题目内容
13. 如图,几个边长皆为1的正方形的一边均在同一条直线上,设△A1A2B2周长为C1,△A1A3B3的周长为C2…△A1An+1Bn+1的周长记为Cn,则Cn=n+1+$\sqrt{{n}^{2}+1}$.
如图,几个边长皆为1的正方形的一边均在同一条直线上,设△A1A2B2周长为C1,△A1A3B3的周长为C2…△A1An+1Bn+1的周长记为Cn,则Cn=n+1+$\sqrt{{n}^{2}+1}$.
分析 根据勾股定理分别求出A1B2、A1B3、A1B4的长,列出各三角形周长算式,根据规律可得.
解答 解:根据题意,∵C1=$\sqrt{{1}^{2}+{1}^{2}}+1+1$=2+$\sqrt{2}$,
C2=$\sqrt{{1}^{2}+{2}^{2}}+1+2$=3+$\sqrt{5}$,
C3=$\sqrt{{1}^{2}+{3}^{2}}+1+3$=4+$\sqrt{10}$,
…
∴Cn=$\sqrt{{1}^{2}+{n}^{2}}+1+n$=n+1+$\sqrt{{n}^{2}+1}$.
故答案为:n+1+$\sqrt{{n}^{2}+1}$.
点评 本题主要考查勾股定理的实际应用和规律的探寻,由勾股定理计算出三角形斜边的长是根本,从已知算式得出规律是关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
3.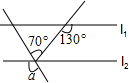 如图,已知直线l1∥l2,则α为( )
如图,已知直线l1∥l2,则α为( )
 如图,已知直线l1∥l2,则α为( )
如图,已知直线l1∥l2,则α为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
4.下列命题是真命题的是( )
| A. | 如果|a|=1那么a=1 | |
| B. | 同位角相等 | |
| C. | 对顶角相等 | |
| D. | 如一个数的绝对值等于它本身则这个数是正数 |