题目内容
6. 如图,在?ABCD中,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
如图,在?ABCD中,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.(1)求证:四边形DMNC是平行四边形;
(2)当AM=AB时,求证:?DMNC是菱形.
分析 (1)由平行四边形的性质得出AB=CD,AD=BC,AD∥BC,由平行线分线段成比例定理和已知条件得出AM=DM=$\frac{1}{2}$AD,同理BN=CN=$\frac{1}{2}$BC,得出DM=CN,即可得出结论;
(2)由平行四边形的性质得出CD=MN,得出MN=AB,证出DM═MN,即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∵AE=AB,
∴$\frac{AE}{BW}=\frac{AM}{BC}$=$\frac{1}{2}$,
∴AM=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴AM=DM=$\frac{1}{2}$AD,
同理:BN=CN=$\frac{1}{2}$BC,
∴DM=CN,
又∵DM∥CN,
∴四边形DMNC是平行四边形;
(2)证明:由(1)得:四边形DMNC是平行四边形,
∴CD=MN,
又∵CD=AB,
∴MN=AB,
∵AM=AB,
∴AM=MN,
∵DM=AM,
∴DM═MN,
∴?DMNC是菱形.
点评 本题考查了平行四边形的判定与性质、菱形的判定、平行线分线段成比例定理;熟练掌握平行四边形的性质,证明DM=MN是解决(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
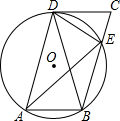 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE. 如图,BC表示河岸,现测得∠ACB=30°,∠ABC=45°,AC=20米,某人位于河岸上的P处,
如图,BC表示河岸,现测得∠ACB=30°,∠ABC=45°,AC=20米,某人位于河岸上的P处, 如图,在平行四边形ABCD中,∠BAD=45°,BD是其一条对角线,AE⊥BD于E,BE=3,DE=2,求平行四边形ABCD的周长?
如图,在平行四边形ABCD中,∠BAD=45°,BD是其一条对角线,AE⊥BD于E,BE=3,DE=2,求平行四边形ABCD的周长? (1)用计算器计算并验证sin25°+sin46°与sin71°之间的大小关系:
(1)用计算器计算并验证sin25°+sin46°与sin71°之间的大小关系: 如图,CD为⊙O的直径,点A在DC的延长线上,直线AE与⊙O切于点B,∠A=28°,求∠DBE的度数.
如图,CD为⊙O的直径,点A在DC的延长线上,直线AE与⊙O切于点B,∠A=28°,求∠DBE的度数. 如图,∠1-∠4=14°,∠1:∠2:∠3=2:3;4.求∠2的度数.
如图,∠1-∠4=14°,∠1:∠2:∠3=2:3;4.求∠2的度数.