题目内容
 如图,y=-5x+5与坐标轴交于A、B两点,△ABC为等腰直角三角形,双曲线y=
如图,y=-5x+5与坐标轴交于A、B两点,△ABC为等腰直角三角形,双曲线y=| k |
| x |
考点:全等三角形的判定与性质,一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征
专题:计算题
分析:由直线y=-5x+5得到A与B坐标,设C坐标为(x,y),根据三角形ABC为等腰直角三角形,列出方程组,求出方程组的解得到C坐标,即可确定出k的值.
解答: 解:∵直线y=-5x+5与坐标轴交于A、B两点,
解:∵直线y=-5x+5与坐标轴交于A、B两点,
∴A(1,0),B(0,5),
设C(x,y),
∵△ABC为等腰直角三角形,
∴AC=BC,即(1-x)2+y2=x2+(y-5)2①,
过点C作CD⊥x轴于点D,
∵CD2+AD2=AC2,2AC2=AB2,即y2+(x-1)2=AC2,2AC2=26,
∴2y2+2(x-1)2=26②,
①②联立得
,
解得y=2或y=3,
由①得,x=5y-12,
当y=2时,x=5×2-12=-2,
当y=3时,x=5×3-13=2(舍去);
∴C(-2,2),
∵点C在反比例函数y=
上,
∴k=-2×2=-4.
 解:∵直线y=-5x+5与坐标轴交于A、B两点,
解:∵直线y=-5x+5与坐标轴交于A、B两点,∴A(1,0),B(0,5),
设C(x,y),
∵△ABC为等腰直角三角形,
∴AC=BC,即(1-x)2+y2=x2+(y-5)2①,
过点C作CD⊥x轴于点D,
∵CD2+AD2=AC2,2AC2=AB2,即y2+(x-1)2=AC2,2AC2=26,
∴2y2+2(x-1)2=26②,
①②联立得
|
解得y=2或y=3,
由①得,x=5y-12,
当y=2时,x=5×2-12=-2,
当y=3时,x=5×3-13=2(舍去);
∴C(-2,2),
∵点C在反比例函数y=
| k |
| x |
∴k=-2×2=-4.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 如图,分别以等腰Rt△ACD的边AD、AC、CD为直径画半圆,求证:所得两个月型图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.
如图,分别以等腰Rt△ACD的边AD、AC、CD为直径画半圆,求证:所得两个月型图案AGCE和DHCF的面积之和(图中阴影部分)等于Rt△ACD的面积.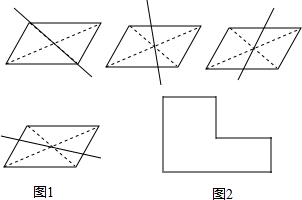 (1)我们知道把平行四边形分成面积相等的两部分的直线有无数条,如图1,这些直线都经过平行四边形的
(1)我们知道把平行四边形分成面积相等的两部分的直线有无数条,如图1,这些直线都经过平行四边形的 如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300
如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300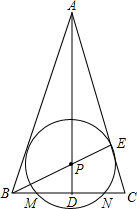 已知△ABC,AB=AC,∠BAC=30°,AD⊥BC于D,E在AC上,BE=BC,BC=2
已知△ABC,AB=AC,∠BAC=30°,AD⊥BC于D,E在AC上,BE=BC,BC=2