题目内容
(1)(4分)计算: .
.
(2)(5分)已知关于x的一元二次方程 有两个相等的实数根,求
有两个相等的实数根,求 的值。
的值。
(1)x1=-5,x2=-4;(2)4
【解析】
试题分析:(1) 先整理成一元二次方程的一般形式,然后进行因式分解,利用因式分解法解方程即可.
(2)由于这个方程有两个相等的实数根,因此△=b2﹣4a=0,可得出a、b之间的关系,然后将 化简后,用含a的代数式表示b,即可求出这个分式的值.
化简后,用含a的代数式表示b,即可求出这个分式的值.
试题解析:(1)由原方程,得
x2+9x+8=-12,
即(x+4)(x+5)=0,
∴x+4=0,或x+5=0,
解得x=-4或x=-5,
∴原方程的根是x1=-5,x2=-4
(2)∵ax2+bx+1=0(a≠0)有两个相等的实数根,
∴△=b2﹣4ac=0,
即b2﹣4a=0,
b2=4a,
∵ =
= =
= =
=
∵a≠0,
∴ =
= =
= =4
=4
考点:1.解一元二次方程-因式分解法;2.根的判别式.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )
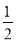
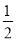 时,y随x的增大而减小
时,y随x的增大而减小 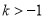 B.
B.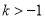 且
且  C.
C.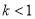 D.
D. 且
且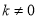
 的方程
的方程 .求证:
.求证: 取任何实数时,方程总有实数根;
取任何实数时,方程总有实数根;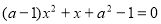 有一个根为0,则a的值是( )
有一个根为0,则a的值是( ) 的小数部分是
的小数部分是 ,
, 的小数部分是
的小数部分是 ,则
,则 = .
= . 中,
中, ,
, 是平面内不与
是平面内不与 、
、 、
、 重合的任意一点,
重合的任意一点, ,
, .
.
 ≌
≌ ;
; 的形状,并证明你的结论.
的形状,并证明你的结论.