题目内容
(8分)已知,如图1, 中,
中, ,
, 是平面内不与
是平面内不与 、
、 、
、 重合的任意一点,
重合的任意一点, ,
, .
.

(1)求证: ≌
≌ ;
;
(2)如图2,当点 是
是 的外接圆圆心时,请判断四边形
的外接圆圆心时,请判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
(1)见解析;
(2)四边形BDCE是菱形,证明见解析.
【解析】
试题分析:(1)由∠ABC=∠DBE可知∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE,根据SAS定理可知△ABD≌△CBE;
(2)由(1)可知,△ABD≌△CBE,故CE=AD,根据点D是△ABC外接圆圆心可知DA=DB=DC,再由BD=BE可判断出BD=BE=CE=CD,故可得出四边形BDCE是菱形.
(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD,
∴∠ABD=∠CBE,
在△ABD与△CBE中,
∵
∴△ABD≌△CBE
(2)解:四边形BDCE是菱形.证明如下:
同(1)可证△ABD≌△CBE,
∴CE=AD,
∵点D是△ABC外接圆圆心,
∴DA=DB=DC,
又∵BD=BE,
∴BD=BE=CE=CD,
∴四边形BDCE是菱形.
考点:三角形的外接圆与外心;全等三角形的判定与性质;菱形的判定.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 .
. 有两个相等的实数根,求
有两个相等的实数根,求 的值。
的值。
 D.
D.

 的直径为3cm,点
的直径为3cm,点 到圆心
到圆心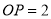 cm,则点
cm,则点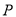 ( )
( ) 的两根之和为( )
的两根之和为( ) B、
B、 C、
C、 D、
D、