题目内容
(5分)已知:关于 的方程
的方程 .求证:
.求证: 取任何实数时,方程总有实数根;
取任何实数时,方程总有实数根;
详见解析
【解析】
试题分析:由判别式△=[-3(m-1)]2-4×m×(2m-3)=m2-6m+9=(m-3)2≥0,即可判定无论m取任何实数时,方程总有实数根;
试题解析:当m=0时,原方程可化为3x-3=0,解得x=1;
当m≠0时,
∵△=[-3(m-1)]2-4×m×(2m-3)=m2-6m+9=(m-3)2≥0,
∴无论m取任何实数时,方程总有实数根;
考点:1.一元一次方程的解;2.根的判别式.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 -4x+2= .
-4x+2= . 的顶点坐标是( )
的顶点坐标是( )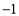 ,3) C.(1,
,3) C.(1,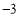 ) D.(
) D.( ,
,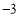 )
)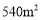 ,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )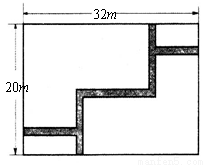
 B.
B. C.
C. D.
D.
 .
. 有两个相等的实数根,求
有两个相等的实数根,求 的值。
的值。
 D.
D.