题目内容
9.(1)解方程:$\frac{x-2}{2x-1}$+1=$\frac{1.5}{1-2x}$;(2)先化简,再求值:$\frac{2x+6}{{x}^{2}-4x+4}$•$\frac{x-2}{{x}^{2}+3x}$-$\frac{1}{x-2}$;其中x=2;
(3)求不等式组$\left\{\begin{array}{l}{\frac{7-x}{2}≥\frac{3+4x}{5}-4}\\{\frac{5}{3}x+5(4-x)≥2(4-x)}\end{array}\right.$的非负整数解.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)原式约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把x的值代入计算即可求出值;
(3)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出非负整数解即可.
解答 解:(1)去分母得:x-2+2x-1=-1.5,
解得:x=-0.5,
经检验x=-0.5是分式方程的解;
(2)原式=$\frac{2(x+3)}{(x-2)^{2}}$•$\frac{x-2}{x(x+3)}$-$\frac{1}{x-2}$=$\frac{2}{x(x-2)}$-$\frac{x}{x(x-2)}$=-$\frac{1}{x}$,
当x=2时,原式=-$\frac{1}{2}$;
(3)不等式组整理得:$\left\{\begin{array}{l}{\frac{7-x}{2}≥\frac{3+4x}{5}-4①}\\{\frac{5}{3}x+5(4-x)≥2(4-x)②}\end{array}\right.$,
由①得:x≤$\frac{69}{13}$,
由②得:x≤9,
∴不等式组的解集为x≤$\frac{69}{13}$,
则不等式组的非负整数解为:0,l,2,3,4,5.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.宁城县打虎石水库,总库容量为11960万立方米,11960万用科学记数法表示为( )
| A. | 1.196×108 | B. | 1.196×107 | C. | 11.96×107 | D. | 0.1196×109 |
14.一个整数加上-15,和大于0,这个整数可能是( )
| A. | 16.5 | B. | 16 | C. | 15 | D. | 14 |
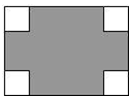 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.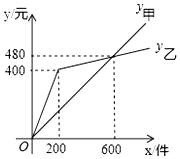 某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售量x(单位:件)的函数关系如图所示,请你根据图象解决下列问题:
某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售量x(单位:件)的函数关系如图所示,请你根据图象解决下列问题: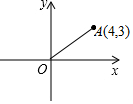 如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个.
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个.