题目内容
19．
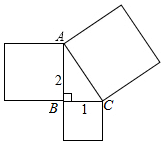如图，分别以Rt△ABC的边为一边向外作正方形，已知AB=2，BC=1．（1）求图中以AC为一边的正方形的面积；
（2）AC的长是不是无理数？若是无理数，请求出它的整数部分？
分析 （1）先根据勾股定理，求得Rt△ABC中的AC边的平方，进而得到以AC为一边的正方形的面积；
（2）根据勾股定理可得，AC的长为无理数$\sqrt{5}$，再根据$\sqrt{4}$＜$\sqrt{5}$＜$\sqrt{9}$求得其整数部分即可．
解答 解：（1）∵Rt△ABC中，AB=2，BC=1，
∴AC2=AB2+BC2=4+1=5，
∴以AC为一边的正方形的面积为5；
（2）∵AC=$\sqrt{5}$，
∴AC的长是无理数，
又∵$\sqrt{4}$＜$\sqrt{5}$＜$\sqrt{9}$，
∴2＜$\sqrt{5}$＜3，
∴$\sqrt{5}$的整数部分为2．
点评 本题主要考查了勾股定理的应用以及无理数的定义，解决问题的关键是掌握：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．解题时注意：无限不循环小数叫做无理数．
练习册系列答案
阅读快车系列答案
相关题目
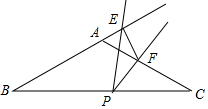如图，在等腰△ABC中，AB=AC=8，∠BAC=120°，P为BC的中点，小慧把含30°角的透明三角板的30°角的顶点放在点P，绕P点旋转，三角板的两边分别交BA的延长线和边AC于点E、F．
如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下五个结论：①AD=BE；②AP=BQ；③DE=DP；④∠AOB=60°．恒成立的结论有几个（ ）