题目内容
14. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③DE=DP;④∠AOB=60°.恒成立的结论有几个( )
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②AP=BQ;③DE=DP;④∠AOB=60°.恒成立的结论有几个( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①只要证明△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),可知②正确;
③首先证明DP=EQ,由DE>QE,且DP=QE,推出DE>DP,(故③错误);
④利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
解答 解:①∵正△ABC和正△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠DAC=∠EBC,(故①正确);
②又∵AC=BC,∠ACP=∠BCQ=60°,∠DAC=∠EBC,
∴△CDP≌△CEQ(ASA).
∴AP=BQ,(故②正确);
③∵△ACP≌△BCQ,
∴AP=QB,
∵△ADC≌△BEC
∴AD=BE,
∴AD-AP=BE-QB,
∴DP=EQ,
∵DE>QE,且DP=QE,
∴DE>DP,(故③错误);
④∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故④正确).
∴正确的有:①②④.
故选C.
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识,正确寻找三角形全等是解答本题的关键,属于中考常考题型.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
4.现有树苗若干棵,计划栽在公路的一侧,要求路的两侧各载一棵,并且每2棵树的间隔距离相等,如果每隔5米栽1棵,则树苗缺21棵.如果每隔5.5米栽一棵,则树苗正好用完.你能算出原来有树苗的棵数和这段路的长度吗?
解:①若相邻两树的间隔长称为一段,那么段数与应植树棵树的关系是段数=植树棵数-1
②相邻两树的间隔长、应植树棵树与路长的关系是路长=(植树棵数-1)×间隔长
③设原有树苗x棵,请你填写下表:
④由于是同一段路上,路长相等,则可列方程5.5(x-1)=5(x+21-1)
解这个方程得x=211
当x=211时,这段路长度为1155米.
解:①若相邻两树的间隔长称为一段,那么段数与应植树棵树的关系是段数=植树棵数-1
②相邻两树的间隔长、应植树棵树与路长的关系是路长=(植树棵数-1)×间隔长
③设原有树苗x棵,请你填写下表:
| 方案 | 间隔长(米) | 应植树数(棵) | 路长(米) |
| 方案1 | 5 | ( ) | ( ) |
| 方案2 | 5.5 | ( x ) | ( ) |
解这个方程得x=211
当x=211时,这段路长度为1155米.
2.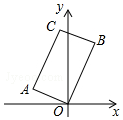 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B点的坐标分别是( )| A. | ($\frac{3}{2}$,3) | B. | ($\frac{3}{2}$,4) | C. | ($\frac{7}{4}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$) |
9.下列说法不正确的是( )
| A. | 圆是轴对称图形 | B. | 圆是中心对称图形 | ||
| C. | 半圆不是弧 | D. | 同圆中,等弧所对的圆心角相等 |
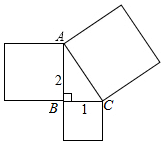 如图,分别以Rt△ABC的边为一边向外作正方形,已知AB=2,BC=1.
如图,分别以Rt△ABC的边为一边向外作正方形,已知AB=2,BC=1.