题目内容
2.不论m取任何实数,抛物线y=(x-m)2+m-1(x为自变量)的顶点都在一条直线上,则这条直线的函数解析式是y=x-1.分析 根据抛物线的顶点式可得顶点坐标,即$\left\{\begin{array}{l}{x=m}&{①}\\{y=m-1}&{②}\end{array}\right.$,①-②得:x-y=1,可知答案.
解答 解:∵抛物线y=(x-m)2+m-1的顶点坐标为(m,m-1),
即$\left\{\begin{array}{l}{x=m}&{①}\\{y=m-1}&{②}\end{array}\right.$,
①-②,得:x-y=1,即y=x-1,
故答案为:y=x-1.
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
13.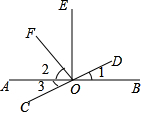 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )
 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )| A. | ∠AOD与∠1互为补角 | B. | ∠1的余角等于74°30′ | ||
| C. | ∠2=45° | D. | ∠DOF=135° |
10.在一次中华好诗词比赛中,某参赛小组的得分如下:95 85 95 85 80 95 90这组数据的中位数和众数分别为( )
| A. | 95 90 | B. | 95 85 | C. | 90 95 | D. | 80 85 |
17.已知x=y,字母m可以取任意有理数,下列等式不一定成立的是( )
| A. | x+m=y+m | B. | x-m=y-m | C. | xm=ym | D. | x+m=x-m |
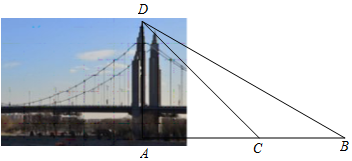
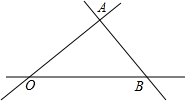 如图,三条公路OA,OB,AB两两相交于点O,点A和点B,现在建一个工厂P,使得工厂P到三条公路的距离相等
如图,三条公路OA,OB,AB两两相交于点O,点A和点B,现在建一个工厂P,使得工厂P到三条公路的距离相等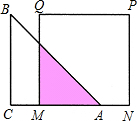 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.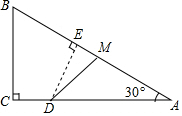 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,点M在AB上,且AM=4,点D是AC边上的一个动点(不与A、C重合),设CD的长为x,△ADM的面积y