题目内容
2．若$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$，则$\frac{2x+y-6z}{5x}$=-$\frac{4}{3}$．分析 设比值为k（k≠0），然后用k表示出x、y、z，再代入比例式进行计算即可得解．
解答 解：设$\frac{x}{3}$=$\frac{y}{4}$=$\frac{z}{5}$=k（k≠0），
则x=3k，y=4k，z=5k，
所以，$\frac{2x+y-6z}{5x}$=$\frac{2•3k+4k-6•5k}{5•3k}$=$\frac{-20k}{15k}$=-$\frac{4}{3}$．
故答案为：-$\frac{4}{3}$．
点评 本题考查了比例的性质，利用“设k法”求解更简便．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
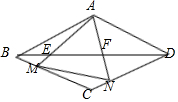已知：菱形ABCD中，∠BAD=120°，M、N分别是BC、CD边上的点，且△AMN是等边三角形．
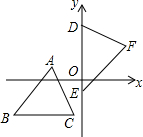如图，坐标平面上，△ABC≌△DEF，且AB=BC=9．若A点的坐标为（-3，1），B、C两点在直线y=-5上，D、E两点在y轴上，则点F到y轴的距离为（ ）
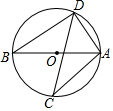如图，AB为⊙O的直径，CD是⊙O的弦，∠ACD=25°，则∠BAD=65°．
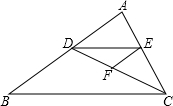如图，已知三角形ABC，点D、E分别在线段AB、AC上，连结DE、CD，F为线段CD上一点，连结EF．∠EFC+∠BDC=180°，∠DEF=∠B，试判断DE与BC的位置关系，并说明理由．
一次函数y1=kx+3与正比例函数y2=-2x交于点A（-1，2）．