题目内容
8.现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.(1)如图1,若点O与点A重合,则OM与ON的数量关系是OM=ON;
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
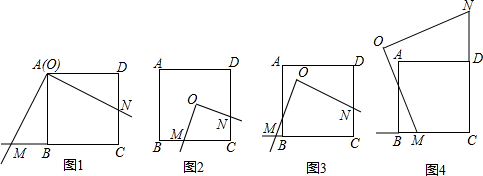
分析 (1)根据△OBM与△ODN全等,可以得出OM与ON相等的数量关系;(2)连接AC、BD,则通过判定△BOM≌△CON,可以得到OM=ON;(3)过点O作OE⊥BC,作OF⊥CD,可以通过判定△MOE≌△NOF,得出OE=OF,进而发现点O在∠C的平分线上;(4)可以运用(3)中作辅助线的方法,判定三角形全等并得出结论.
解答  解:(1)若点O与点A重合,则OM与ON的数量关系是:OM=ON;
解:(1)若点O与点A重合,则OM与ON的数量关系是:OM=ON;
(2)仍成立.
证明:如图2,连接AC、BD,则
由正方形ABCD可得,∠BOC=90°,BO=CO,∠OBM=∠OCN=45°
∵∠MON=90°
∴∠BOM=∠CON
在△BOM和△CON中
$\left\{\begin{array}{l}{∠OBM=∠OCN}\\{BO=CO}\\{∠BOM=∠CON}\end{array}\right.$
∴△BOM≌△CON(ASA)
∴OM=ON
(3)如图3,过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,则∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中
$\left\{\begin{array}{l}{∠OEM=∠OFN}\\{∠MOE=∠NOF}\\{OM=ON}\end{array}\right.$
∴△MOE≌△NOF(AAS)
∴OE=OF
又∵OE⊥BC,OF⊥CD
∴点O在∠C的平分线上
∴O在移动过程中可形成线段AC
(4)O在移动过程中可形成直线AC.
点评 本题主要考查了四边形中的正方形,解决问题的关键是作辅助线构造全等三角形.解题时需要运用全等三角形的判定与性质,以及角平分线的判定定理.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
19.与$\sqrt{2}$是同类二次根式的为( )
| A. | $\sqrt{8}$ | B. | $\sqrt{3}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
3.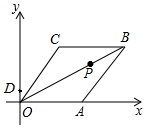 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )| A. | (0,0) | B. | (1,$\frac{1}{2}$) | C. | ($\frac{6}{5}$,$\frac{3}{5}$) | D. | ($\frac{10}{7}$,$\frac{5}{7}$) |
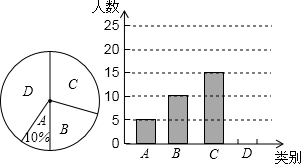
20. 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
请根据上述统计图表,解答下列问题:
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
 秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:| 分 数 段 | 频数 | 频率 |
| 60≤x<70 | 9 | a |
| 70≤x<80 | 36 | 0.4 |
| 80≤x<90 | 27 | b |
| 90≤x≤100 | c | 0.2 |
(1)在表中,a=0.1,b=0.3,c=18;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?
17.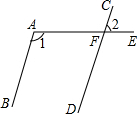 如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
 如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |

 如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.
如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长为16cm.