题目内容
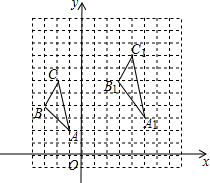
 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为
如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为考点:二次函数的最值,二次函数图象上点的坐标特征
专题:
分析:设P(x,y)(2>x>0,y>0),根据矩形的周长公式得到C=-2(x-1)2+6.根据二次函数的性质来求最值即可.
解答:解:∵y=-x2+x+2,
∴当y=0时,-x2+x+2=0即-(x-2)(x+1)=0,
解得 x=2或x=-1
故设P(x,y)(2>x>0,y>0),
∴C=2(x+y)=2(x-x2+x+2)=-2(x-1)2+6.
∴当x=1时,C最大值=6,.
即:四边形OAPB周长的最大值为6.
故答案是:6.
∴当y=0时,-x2+x+2=0即-(x-2)(x+1)=0,
解得 x=2或x=-1
故设P(x,y)(2>x>0,y>0),
∴C=2(x+y)=2(x-x2+x+2)=-2(x-1)2+6.
∴当x=1时,C最大值=6,.
即:四边形OAPB周长的最大值为6.
故答案是:6.
点评:本题考查了二次函数的最值,二次函数图象上点的坐标特征.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题采用了配方法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图:
如图: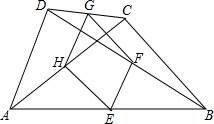 如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.

 如图是一款可折叠的木制宝宝画板.已知AB=AC=67cm,BC=30cm,则∠ABC的大小约为
如图是一款可折叠的木制宝宝画板.已知AB=AC=67cm,BC=30cm,则∠ABC的大小约为