题目内容
如图，正三角形的内切圆中的内接正方形的边长为2，则正三角形的边长为（ ）A、
| ||
B、2
| ||
C、2
| ||
D、2
|
考点：正多边形和圆
专题：
分析：利用正方形的性质得出圆的半径，进而求出AE的长即可得出答案．
解答：
解：如图所示：设正方形的中心为O，E为切点，连接EO，AO，
则圆的半径为：2sin45°=
，
即EO=
，故AO=2
，
则AE=
=
，
故正三角形的边长为：2
．
故选：D．
解：如图所示：设正方形的中心为O，E为切点，连接EO，AO，则圆的半径为：2sin45°=
| 2 |
即EO=
| 2 |
| 2 |
则AE=
| AO2-EO2 |
| 6 |
故正三角形的边长为：2
| 6 |
故选：D．
点评：此题主要考查了正多边形和圆，根据题意得出圆的半径是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在平面直角坐标系xOy中，点A（0，5），点B（6，5）．在
，
，
，-
，3.
，3.1415，2.010101…（相邻两个1之间有1个0）中，无理数有（ ）
| 25 |
| 2 |
| 11 |
| 3 |
| π |
| 3 |
| •• |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
用科学记数法表示9 270 000正确的是（ ）
| A、9.27×106 |
| B、9.27×105 |
| C、9.27×104 |
| D、927×103 |
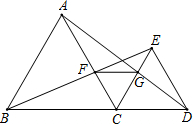如图，已知点C在线段BD上，在BD的同侧作正△CDE、正△ABC，AC交BE于F，AD交CE于G，连接FG，在这个图形中，不在标注其它字母和添加任何辅助线，由这些条件可推出哪些结论？