题目内容
如图，直线
、
、
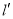表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有( )
A. 一处 B. 二处 C. 三处 D. 四处
D
【解析】如图所示，加油站站的地址有四处.
故选：D.
练习册系列答案
相关题目
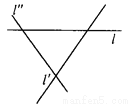
在边长为1个单位长度的小正方形组成的网格中，点A、B、C、O都是格点．
（1）将△ABC向左平移6个单位得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
（1）作图见解析；（2）作图见解析.
【解析】试题分析：（1）把A、B、C三点分别向左平移6个单位长度，即可得到三个顶点的对应点，然后顺次连接三点即可；
（2）连接AO并延长，然后截取OA2=OA，则A2就是A的对应点，同样可以作出B、C的对应点，然后顺次连接即可．
【解析】
（1）所作图形如图所示；
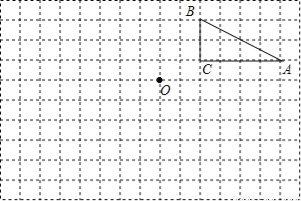
（2）所作图形如图所示． 二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C
【解析】试题分析：根据抛物线的顶点在第四象限，得出n＜0，m＜0，即可得出一次函数y=mx+n的图象经过二、三、四象限．
故选C． 已知：如图，△ABC的∠B、∠C的平分线相交于点D，过D作MN∥BC交AB、AC分别于点M、N，求证：BM＋CN＝MN.
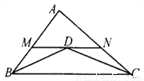
见解析
【解析】试题分析：根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠6=∠2，∠3=∠5，然后求出∠1=∠6，∠4=∠5，根据等角对等边的性质可得BM=DM，CN=DN，然后列式求解即可得证．
试题解析：证明：
∵BD、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠3=∠4，
∵MN∥BC，
∴∠6=∠2，∠3=∠5，
... 在Rt△ABC中，锐角∠A的平分线与锐角∠B的平分线相交于点D，则∠ADB＝______．
135°
【解析】在Rt△ABC中,∠CAB+∠CBA=180°?90°=90°，
∵锐角∠A的平分线与锐角∠B的平分线相交于点D，
∴∠DAB+∠DBA= (∠CAB+∠CBA)= ×90°=45°，
在△ABD中,∠ADB=180°?(∠DAB+∠DBA)=180°?45°=135°
故答案为：135°. 下列判断正确的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 有两边对应相等，且有一角为30°的两个等腰三角形全等
C. 有一角和一条边对应相等的两个直角三角形全等
D. 有两角和一边对应相等的两个三角形全等
D
【解析】A.只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时，才能成立；
B. 30°角没有对应关系，不能成立；
C.如果这个角是直角，此时就不成立了；
D.符合全等三角形的判断方法：AAS或者ASA.
故选：D. 分解因式：16(x－y)2－9(x＋y)2.
(7x－y)(x－7y)
【解析】试题分析:利用平方差公式因式分解即可.
试题解析:
16(x－y)2－9(x＋y)2
=[4(x－y)－3(x＋y)][4(x－y)+3(x＋y)]
=(x－7y)(7x－y). 将抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为 ．
y=2﹣2
【解析】试题分析：按照“左加右减，上加下减”的规律可得抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y=2（x﹣1+3）2+2﹣4=2（x+2）2﹣2．即可得抛物线的解析式为y=2（x+2）2﹣2． 如图，直线y＝－2x与直线y＝kx＋b相交于点A(a,2)，并且直线y＝kx＋b经过x轴上点B(2,0)．
(1)求直线y＝kx＋b的解析式；
(2)求两条直线与y轴围成的三角形面积；
(3)直接写出不等式(k＋2)x＋b≥0的解集．
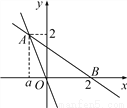
（1）一次函数的解析式是y＝－x＋；（2）S△ABC＝；（3）x≥－1.
【解析】试题分析：利用代入法求出点A的坐标，然后根据待定系数法求出一次函数的解析式；
（2）根据图像求出交点C的坐标，然后可求三角形的面积；
（3）根据图像的位置求出不等式的解集.
试题解析：【解析】
(1)把A(a,2)代入y＝－2x中，得－2a＝2，∴a＝－1，∴A(－1,2)，把A(－1,2)...