题目内容
抛物线y=﹣(x+2)2﹣3的顶点坐标是( )
A. (2,﹣3) B. (﹣2,3) C. (2,3) D. (﹣2,﹣3)
 D
【解析】试题分析:∵抛物线y=﹣(x+2)2﹣3为抛物线解析式的顶点式,∴抛物线顶点坐标是(﹣2,﹣3).故选D.
D
【解析】试题分析:∵抛物线y=﹣(x+2)2﹣3为抛物线解析式的顶点式,∴抛物线顶点坐标是(﹣2,﹣3).故选D.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,锐角∠A的平分线与锐角∠B的平分线相交于点D,则∠ADB=______.
 135°
【解析】在Rt△ABC中,∠CAB+∠CBA=180°?90°=90°,
∵锐角∠A的平分线与锐角∠B的平分线相交于点D,
∴∠DAB+∠DBA= (∠CAB+∠CBA)= ×90°=45°,
在△ABD中,∠ADB=180°?(∠DAB+∠DBA)=180°?45°=135°
故答案为:135°.
135°
【解析】在Rt△ABC中,∠CAB+∠CBA=180°?90°=90°,
∵锐角∠A的平分线与锐角∠B的平分线相交于点D,
∴∠DAB+∠DBA= (∠CAB+∠CBA)= ×90°=45°,
在△ABD中,∠ADB=180°?(∠DAB+∠DBA)=180°?45°=135°
故答案为:135°. 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过( )
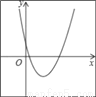
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
 C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C.
C
【解析】试题分析:根据抛物线的顶点在第四象限,得出n<0,m<0,即可得出一次函数y=mx+n的图象经过二、三、四象限.
故选C. 如图在平面直角坐标系中,二次函数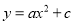 的图象过正方形ABOC的三个顶点A、B、C,则
的图象过正方形ABOC的三个顶点A、B、C,则 值为__________。
值为__________。
 -2
【解析】试题解析:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=-,
则ac=-•2m=-2.
-2
【解析】试题解析:设正方形的对角线OA长为2m,
则B(-m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=-,
则ac=-•2m=-2. 若二次函数y=ax2-2ax+c的图象经过点(-1,0),则方程ax2-2ax+c=0的解为 ( )
A. x1=-3,x2=-1 B. x1=1,x2=3 C. x1=-1,x2=3 D. x1=-3,x2=1
 C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3.
C
【解析】试题分析:根据题意可得:二次函数的对称轴为直线x=1,则函数与x轴的交点坐标为(-1,0)和(3,0),则方程的解为x=-1或x=3. 如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.
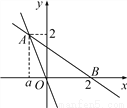
 (1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)...
(1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:【解析】
(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)... 不等式组 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
A. 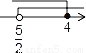 B.
B. 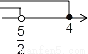 C.
C. 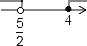 D.
D. 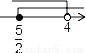
 A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A.
A
【解析】解不等式x-1≤7-x得x≤4;
解不等式5x-2>3(x+1)得x>,
所以<x≤4.
在数轴上表示正确的是A.
故选A. 在等腰梯形ABCD中,AD∥BC,AE⊥BC于E,且AE=AD,BC=3AE, 则∠BAD等于 ( )
A. 120° B. 135° C. 130° D. 不能确定
 B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B.
B
【解析】【解析】
过点D作DF⊥BC于点F.
∵AE⊥BC,DF⊥BC,AD=AE,∴四边形AEFD为正方形,∴AD=EF.
∵AD=AE,BC=3AD,∴BE=AE=EF=FC,∴∠B=45°,∴∠BAD=135°.
故选B. 不等式2x<7的解有_____个,其中非负整数解有___个.
 无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4.
无数 4
【解析】解不等式2x<7可得x<,所以不等式有无数各界,其中非负整数解有0、1、2、3,共4个.
故答案为:无数,4. 
