题目内容
8.(1)计算:$|{-\sqrt{2}}|+{(-\frac{1}{2})^{-1}}sin45°+{(\sqrt{2014})^0}$;(2)解方程:(x+2)2=3(x+2).
分析 (1)分别根据0指数幂及负整数指数幂的运算法则、绝对值的性质分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先移项,再用因式分解法求出x的值即可.
解答 解:(1)原式=$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$+1
=$\sqrt{2}$-$\sqrt{2}$+1
=1;
(2)原方程可化为:(x+2)2-3(x+2)=0,即(x+2)(x-1)=0.
解得x1=-2,x2=1.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的运算法则、绝对值的性质是解答此题的关键.

练习册系列答案
相关题目
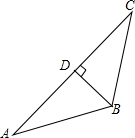 如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,在△ABC中,BD⊥AC于点D,若BC=10,AC=20,∠C=37°,求AB的长.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面和左面看到的几何体的形状图.
如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面和左面看到的几何体的形状图. 如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF.
如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF.