题目内容
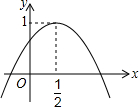 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(| 1 |
| 2 |
| A、① | B、② | C、③ | D、④ |
考点:二次函数图象与系数的关系
专题:
分析:①根据抛物线与y轴的交点坐标即可确定;
②根据抛物线与x轴的交点情况即可判定;
③根据抛物线的对称轴即可判定;
④根据抛物线的顶点纵坐标即可判定.
②根据抛物线与x轴的交点情况即可判定;
③根据抛物线的对称轴即可判定;
④根据抛物线的顶点纵坐标即可判定.
解答:解:①抛物线与y轴正半轴相交,∴c>0,故①正确;
②抛物线与x轴相交于两个交点,∴b2-4ac>0,故②正确;
③∵抛物线的对称轴为x=
,∴x=-
=
,∴a+b=0,故③正确;
④∵抛物线顶点的纵坐标为1,∴
=1,∴4ac-b2=4a,故④错误;
其中错误的是④.
故选D.
②抛物线与x轴相交于两个交点,∴b2-4ac>0,故②正确;
③∵抛物线的对称轴为x=
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
④∵抛物线顶点的纵坐标为1,∴
| 4ac-b2 |
| 4a |
其中错误的是④.
故选D.
点评:此题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数的自变量与对应的函数值,顶点坐标的熟练运用.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为
如图,正方形ABCD的边长为 如图,在一个四边形各边上任意取一点,并顺次连接它们,想一想,你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
如图,在一个四边形各边上任意取一点,并顺次连接它们,想一想,你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?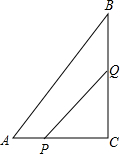 如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点Q是线段BC的中点,点P从A开始沿AC边向C以1cm/s的速度移动.问:经过几秒钟,四边形APQB的面积是16cm2?
如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,点Q是线段BC的中点,点P从A开始沿AC边向C以1cm/s的速度移动.问:经过几秒钟,四边形APQB的面积是16cm2?