题目内容
10.计算(1)${(-\frac{1}{2})^{-2}}-{2^3}×0.125+{2007^0}$
(2)$\frac{3y}{2x+2y}+\frac{2xy}{{{x^2}+xy}}$
(3)($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用乘方的意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果;
(3)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=4-1+1=4;
(2)原式=$\frac{3y}{2(x+y)}$+$\frac{2xy}{x(x+y)}$=$\frac{3y}{2(x+y)}$+$\frac{4y}{2(x+y)}$=$\frac{7y}{2(x+y)}$;
(3)原式=-[$\frac{a}{(a+b)(a-b)}$-$\frac{a-b}{(a+b)(a-b)}$]•$\frac{a-b}{b}$=-$\frac{b}{(a+b)(a-b)}$•$\frac{a-b}{b}$=-$\frac{1}{a+b}$.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
18. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A. | 45° | B. | 60° | C. | 90° | D. | 30° |
5. 如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
 如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )
如图,直线AB、CD相交于O,OB是∠DOE的平分线,若∠COE=100°,则∠AOC=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
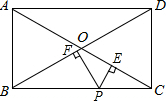 已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.
已知矩形ABCD对角线AC,BD交于点O,点P为BC边上任意一点,PE⊥AC于点E,PF⊥BD于点F,∠AOD=120°,AC=8,求PE+PF的值.



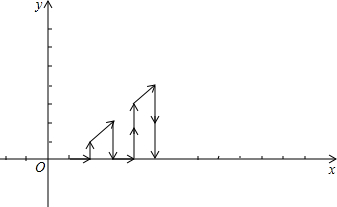 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).