题目内容
2.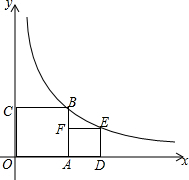 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)
分析 在正方形中四边都相等,由反比例的性质可知S□OABC=4,即OA=2.若假设点E的纵坐标为m,则横坐标为2+m,因为在反比例函数图象上任意一点的横坐标和纵坐标之积都等于比例系数k=4,所以可列方程进行解答.
解答 解:依据比例系数k的几何意义可得正方形OABC的面积为4,
则其边长为2,
设点E的纵坐标为m,则横坐标为2+m,
则m(2+m)=4,
解得m1=$\sqrt{5}$-1,m2=-$\sqrt{5}$-1(不合题意,舍去),
故m=$\sqrt{5}$-1.
2+m=$\sqrt{5}$+1,
故点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1).
故答案为:$\sqrt{5}$+1,$\sqrt{5}$-1.
点评 此题考查了反比例函数图象上点的坐标特征,以比例系数k的几何意义为知识基础,结合正方形的面积设计了一道中考题,由此也可以看出比例系数k的几何意义在解答问题中的重要性.

练习册系列答案
相关题目
1.化简$\frac{{a}^{2}}{a-1}+\frac{1}{1-a}$的结果是( )
| A. | a | B. | a+1 | C. | a-1 | D. | a2-1 |
14.下列式子一定是二次根式的是( )
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
11.下列说法中正确的是:所有的( )都相似.
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
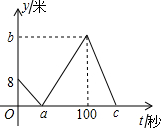 小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法:
小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法: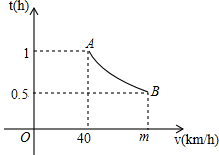 某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).
某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).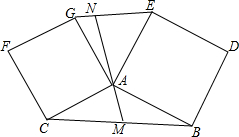 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.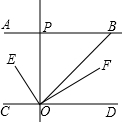 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论: