题目内容
12.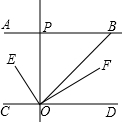 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=$\frac{1}{2}$(180-a)°;
②OF平分∠BOD;
③∠POE=∠BOF;
④∠POB=2∠DOF.
其中正确的个数有多少个?( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由于AB∥CD,则∠ABO=∠BOD=40°,利用平角等于得到∠BOC=(180-a)°,再根据角平分线定义得到∠BOE=$\frac{1}{2}$(180-a)°;利用OF⊥OE,可计算出∠BOF=$\frac{1}{2}$a°,则∠BOF=$\frac{1}{2}$∠BOD,即OF平分∠BOD; 利用OP⊥CD,可计算出∠POE=$\frac{1}{2}$a°,则∠POE=∠BOF; 根据∠POB=90°-a°,∠DOF=$\frac{1}{2}$a°,可知④不正确.
解答 解:①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°-a°=(180-a)°,
又∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠COB=$\frac{1}{2}$(180-a)°,故①正确;
②∵OF⊥OE,
∴∠EOF=90°,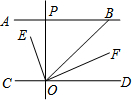
∴∠BOF=90°-$\frac{1}{2}$(180-a)°=$\frac{1}{2}$a°,
∴∠BOF=$\frac{1}{2}$∠BOD,
∴OF平分∠BOD,所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°-∠EOC=$\frac{1}{2}$a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°-a°,
而∠DOF=$\frac{1}{2}$a°,所以④错误.
故选:C.
点评 本题考查了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补;两直线平行,同位角相等.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
17. 如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )
如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )
 如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )
如图,已知直线a,b被线段AB所截,则其中属于内错角的是( )| A. | ∠2和∠3 | B. | ∠1和∠3 | C. | ∠1和∠4 | D. | ∠2和∠4 |
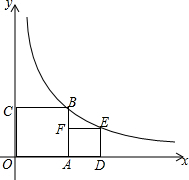 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)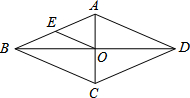 在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.
在菱形ABCD中,E为AB的中点,OE=3,则菱形ABCD的周长为24.