题目内容
2. 如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.
如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.从中任选两个作为条件,另一个作为结论,共可编出几个真命题,并选一个加以证明.
分析 可以写出三个真命题:(1)①②⇒③;(2)①③⇒②;(3)②③⇒①.利用平行线的判定与性质对(1)进行证明.
解答 解:真命题有:(1)①②⇒③;(2)①③⇒②;(3)②③⇒①.
证明(1)的过程为:
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴AC∥BD,
∴∠E=∠F;
证明(2)的过程为:
∵∠E=∠F,
∴AC∥BD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∴∠C=∠B;
证明(3)的过程为:
∵∠E=∠F,
∴AC∥BD,
∴∠B+∠CAB=∠C+∠CDB=180°,
∵∠C=∠B,
∴∠CAB=∠CDB,
∴四边形ABCD是平行四边形,
∴AB∥CD.
点评 本题考查了命题与定理:命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
17.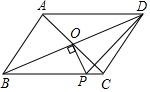 如图,在周长为30的?ABCD中,AB≠AD,AC、BD相交于点O,OP⊥BD,交BC于点P,则△PCD的周长为( )
如图,在周长为30的?ABCD中,AB≠AD,AC、BD相交于点O,OP⊥BD,交BC于点P,则△PCD的周长为( )
 如图,在周长为30的?ABCD中,AB≠AD,AC、BD相交于点O,OP⊥BD,交BC于点P,则△PCD的周长为( )
如图,在周长为30的?ABCD中,AB≠AD,AC、BD相交于点O,OP⊥BD,交BC于点P,则△PCD的周长为( )| A. | 7.5 | B. | 10 | C. | 15 | D. | 20 |
7.已知一次函数y=kx+m-2x与y轴的负半轴相交,且函数值y随x增大而减小,则下列结论正确的是( )
| A. | k<2,m>0 | B. | k<2,m<0 | C. | k>2,m>0 | D. | k>2,m<0 |
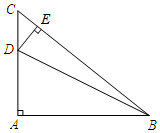 如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$.
如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$.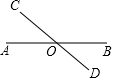 如图所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为62°.
如图所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为62°. 如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,若∠1=25°,则∠2的度数是115°.
如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,若∠1=25°,则∠2的度数是115°.