题目内容
14.a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=3,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2009=-$\frac{1}{2}$.分析 根据差倒数的定义分别求出前几个数便不难发现,每3个数为一个循环组依次循环,用2009除以3,根据余数的情况确定出与a2009相同的数即可得解.
解答 解:∵a1=3,
∴a2=$\frac{1}{1-3}$=-$\frac{1}{2}$,
a3=$\frac{1}{1-(-\frac{1}{2})}$=$\frac{2}{3}$,
a4=$\frac{1}{1-\frac{2}{3}}$=3,
…
数字3、-$\frac{1}{2}$、$\frac{2}{3}$依次不断循环出现,
2009÷3=669…2.
∴a2009与a2相同,为-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查数字变化规律,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4.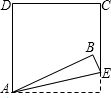 如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
 如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比大∠BAE大48°.设∠BAD和∠BAE的度数分别为x、y,那么x、y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}{y-x=48}\\{y+x=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=48}\\{y=2x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-x=48}\\{y+2x=90}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=48}\\{x+2y=90}\end{array}\right.$ |
6.下列说法中正确的是( )
| A. | 正数和负数统称有理数 | B. | 若|a|=|b|,则a=b. | ||
| C. | -0.210×510=(-0.2×5)10=1 | D. | x是有理数,则x2+1永远是正数 |
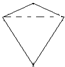
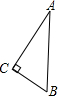 将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )
将如图所示放置的一个直角三角形ABC,(∠C=90°),绕斜边AB旋转一周,所得到的几何体的正视图是下面四个图中的( )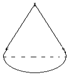
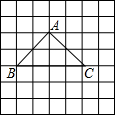 如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).
如图,△ABC的点A的坐标是(3,4),点B的坐标是(1,2).