题目内容
17．
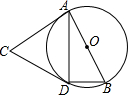如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD．若∠ACD=48°，则∠DBA的大小是（ ）| A． | 48° | B． | 60° | C． | 66° | D． | 32° |
分析 构建切线长定理可知CA=CD，求出∠CAD，再证明∠DBA=∠CAD即可解决问题．
解答 解：∵CA、CD是⊙O的切线，
∴CA=CD，
∵∠C=48°，
∴∠CAD=∠CDA=66°，
∵CA⊥AB，AB是直径，
∴∠ADB=∠CAB=90°，
∴∠DBA+∠DAB=90°，∠CAD+∠DAB=90°，
∴∠DBA=∠CAD=66°，
故选C．
点评 本题考查切线的性质、等腰三角形的性质、直径所对的圆周角是直角等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
7．将抛物线y=-2x2先向左平移1个单位，再向上平移3个单位，两次平移后得到的抛物线的解析式为（ ）
| A． | y=-2（x+1）2+3 | B． | y=-2（x+1）2-3 | C． | y=-2（x-1）2+3 | D． | y=-2（x-1）2-3 |
8．下面数据中，是精确数据的是（ ）
| A． | 2002年美国在阿富汗的战争中每月耗费10亿美元 | |
| B． | 人的大脑有10000000000个细胞 | |
| C． | 小明买了5本小说 | |
| D． | 有关部门预测，2012年以DVD形式出售的影片将首次超过盒式录像带，达到95亿美元 |
5．
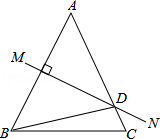如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A的度数是（ ）
如图，等腰△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，∠DBC=15°，则∠A的度数是（ ）| A． | 35° | B． | 40° | C． | 50° | D． | 55° |
12．
如图所示，线段AC的垂直平分线交AB于点D，∠A=43°，则∠BDC的度数为（ ）
如图所示，线段AC的垂直平分线交AB于点D，∠A=43°，则∠BDC的度数为（ ）| A． | 90° | B． | 60° | C． | 86° | D． | 43° |
9．八（3）班第四组10名同学在“爱心捐款”活动中，捐款情况统计如下表，则捐款数组成的数据中，中位数与众数分别是（ ）
| 捐款（元） | 5 | 10 | 50 | 100 |
| 人数 | 1 | 4 | 3 | 2 |
| A． | 100，50 | B． | 30，10 | C． | 10，10 | D． | 10，50 |
