题目内容
5.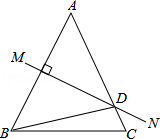 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )| A. | 35° | B. | 40° | C. | 50° | D. | 55° |
分析 由AB的垂直平分线MN交AC于点D,可得AD=BD,即可证得∠ABD=∠A,又由等腰△ABC中,AB=AC,可得∠ABC=$\frac{′80°-∠A}{2}$,继而可得:$\frac{180°-∠A}{2}$-∠A=15°,解此方程即可求得答案.
解答 解:∵DM是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A,
∵等腰△ABC中,AB=AC,
∴∠ABC=∠C=$\frac{′80°-∠A}{2}$,
∴∠DBC=∠ABC-∠ABD=$\frac{′80°-∠A}{2}$-∠A=15°,
解得:∠A=50°.
故选C.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等,注意方程思想的应用.

练习册系列答案
相关题目
15.对于多项式x2-2x-18,下列说法中正确的是( )
| A. | 它是二次三项式 | B. | 它的常数项是18 | ||
| C. | 它的一次项系数是-2x | D. | 它的二次系数是0 |
16. 如图,数轴上的点A表示的数为x,化简|x|+|1-x|的结果为( )
如图,数轴上的点A表示的数为x,化简|x|+|1-x|的结果为( )
 如图,数轴上的点A表示的数为x,化简|x|+|1-x|的结果为( )
如图,数轴上的点A表示的数为x,化简|x|+|1-x|的结果为( )| A. | 1 | B. | 2x-1 | C. | 2x+1 | D. | 1-2x |
20.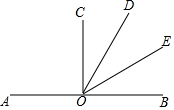 如图,O是直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有( )
如图,O是直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有( )
 如图,O是直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有( )
如图,O是直线AB上一点,∠AOD=120°,∠AOC=90°,OE平分∠BOD,则图中彼此互补的角共有( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
10.下列轴对称图形中,对称轴的数量小于3的是( )
| A. |  | B. |  | C. |  | D. |  |
17.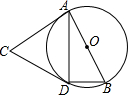 如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
 如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )| A. | 48° | B. | 60° | C. | 66° | D. | 32° |