题目内容
12．
如图所示，线段AC的垂直平分线交AB于点D，∠A=43°，则∠BDC的度数为（ ）| A． | 90° | B． | 60° | C． | 86° | D． | 43° |
分析 根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到∠DCA=∠A，根据三角形的外角的性质计算即可．
解答 解：∵DE是线段AC的垂直平分线，
∴DA=DC，
∴∠DCA=∠A=43°，
∴∠BDC=∠DCA+∠A=86°，
故选：C．
点评 本题考查的是线段垂直平分线的性质和三角形的外角的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
步步高达标卷系列答案
相关题目
2．方程x2-4x=0的解是（ ）
| A． | x1=-2，x2=2 | B． | x=4 | C． | x1=0，x2=4 | D． | x1=-4，x2=4 |
3．已知点D，E，F分别是△ABC三边的中点，若△ABC的周长是30cm，那么△DEF的周长是（ ）
| A． | 15cm | B． | 10cm | C． | 20cm | D． | 18cm |
20．
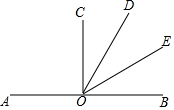如图，O是直线AB上一点，∠AOD=120°，∠AOC=90°，OE平分∠BOD，则图中彼此互补的角共有（ ）
如图，O是直线AB上一点，∠AOD=120°，∠AOC=90°，OE平分∠BOD，则图中彼此互补的角共有（ ）| A． | 4对 | B． | 5对 | C． | 6对 | D． | 7对 |
7．
如图，下列描述正确的是（ ）
如图，下列描述正确的是（ ）| A． | 射线OA的方向是北偏东方向 | B． | 射线OB的方向是北偏西65° | ||
| C． | 射线OC的方向是东南方向 | D． | 射线OD的方向是西偏南15° |
17．
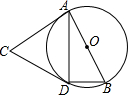如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD．若∠ACD=48°，则∠DBA的大小是（ ）
如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A、D为切点，连接BD、AD．若∠ACD=48°，则∠DBA的大小是（ ）| A． | 48° | B． | 60° | C． | 66° | D． | 32° |
李明同学要证明命题“三角形的中位线平行于三角形的第三边，并且等于第三边的一半”，他已经画出了图形，写出已知和求证，并请你帮助他写出证明过程．