题目内容
已知一矩形的两边长分别为7cm和12cm,其中一个内角的平分线分长边为两部分,这两部分的长分别为( )
| A、6cm和6cm |
| B、7cm和5cm |
| C、4cm和8cm |
| D、3cm和9cm |
考点:矩形的性质
专题:
分析:根据已知条件以及矩形性质证△ABE为等腰三角形得到AB=AE,注意“长和宽分别为7cm和12cm”说明有2种情况,需要分类讨论.
解答:解:∵矩形ABCD中,BE是角平分线.
∴∠ABE=∠EBC.
∵AD∥BC.
∴∠AEB=∠EBC.
∴∠AEB=∠ABE
∴AB=AE.
当AB=12cm时:则AE=12cm,不满足题意.
当AB=7cm时:AE=7cm,则DE=5cm.
故选B.
∴∠ABE=∠EBC.

∵AD∥BC.
∴∠AEB=∠EBC.
∴∠AEB=∠ABE
∴AB=AE.
当AB=12cm时:则AE=12cm,不满足题意.
当AB=7cm时:AE=7cm,则DE=5cm.
故选B.
点评:此题考查了矩形的性质与等腰三角形的判定与性质.注意出现角平分线,出现平行线时,一般出现等腰三角形,需注意等腰三角形相等边的不同.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,AB=AC,∠AOC=60°,则∠ACB的大小是( )| A、30° | B、45° |
| C、60° | D、70° |
在△ABC中,AB=AC,若AC的垂直平分线DE交AC于点D,交BC于点E,且∠BAE=90°,则∠B为( )
| A、60° | B、30° |
| C、45° | D、无法确定 |
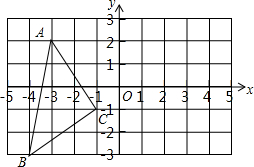 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).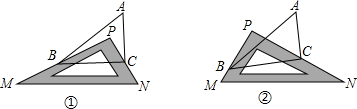
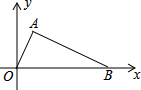 如图,已知A(1,2),B(5,0),O(0,0),试判断△ABO的形状,并说明理由.
如图,已知A(1,2),B(5,0),O(0,0),试判断△ABO的形状,并说明理由.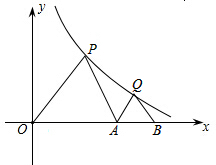 △POA、△QAB都是等边三角形,点P、Q都在双曲线y=
△POA、△QAB都是等边三角形,点P、Q都在双曲线y=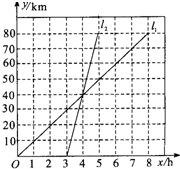 如图表示小王骑自行车和小李骑摩托车都沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题:
如图表示小王骑自行车和小李骑摩托车都沿相同的路线由甲地到乙地行驶过程的函数图象,两地相距80千米,请根据图象解决下列问题: