题目内容
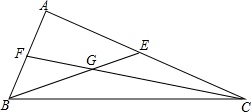如图，△ABC的中线BE、CF相交于G，且AB=12，AC=16，BC=20，求GC的长．考点：三角形中位线定理,勾股定理的逆定理
专题：
分析：首先利用勾股定理的逆定理可判定△ABC是直角三角形，所以可求出CF的长，又因为G是△ABC重心，所以CG可求出．
解答：解：∵AB=12，AC=16，BC=20，
∴AB2+AC2=BC2，
∴△ABC是直角三角形，
∴∠A=90°，
∵F是AB中点，
∴AF=6，
∴CF=
=
=2
，
∵中线BE、CF相交于G，
∴G是△ABC重心，
∴CG：GF=2：1，
∴CG=
．
∴AB2+AC2=BC2，
∴△ABC是直角三角形，
∴∠A=90°，
∵F是AB中点，
∴AF=6，
∴CF=
| AF2+AC2 |
| 292 |
| 73 |
∵中线BE、CF相交于G，
∴G是△ABC重心，
∴CG：GF=2：1，
∴CG=
4
| ||
| 3 |
点评：本题考查了勾股定理以及其逆定理的运用和三角形重心的性质，题目的综合性较强，难度中等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列各组数中，是勾股数的是（ ）
| A、12，8，5 | ||||||
| B、3，4，5 | ||||||
| C、9，13，15 | ||||||
D、
|
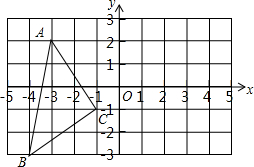如图，在平面直角坐标系中，A（-3，2），B（-4，-3），C（-1，-1）．