题目内容
18.探究:如图①,△ABC是等边三角形,AD是BC边上的高线,以点D为中点作线段EF,且EF不与BC边重合,以EF为边作等边三角形EFG,连结AG,GD,CF.求证:△ADG∽△CDF;应用:如图②,将线段EF绕着点D逆时针旋转,当点F落在AD上时,延长CF交AG于点H,求∠AHF的度数.
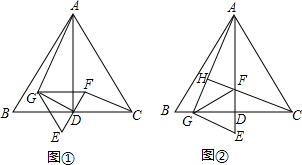
分析 探究:如图①由△ABC是等边三角形,D是EF的中点,于是得到GD⊥EF,由于AD⊥BC,推出∠ADF+∠ADG=∠CDF+∠ADF,于是得到∠ADG=∠CDF,根据△ABC与△EFG是等边三角形,得到△ABC∽△EFG,根据相似三角形的性质得到$\frac{AD}{GD}=\frac{CD}{DF}$,即可得到结论;
应用:如图②,根据相似三角形的性质得到∠GAD=∠FCD,由于∠FDC=90°,∠AFH=∠CFD,于是得到∠GAD+∠AFH=∠FCD+∠CFD=90°,即可得到结果.
解答 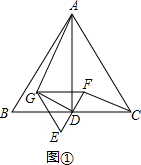 解:探究:如图①∵△ABC是等边三角形,D是EF的中点,
解:探究:如图①∵△ABC是等边三角形,D是EF的中点,
∴GD⊥EF,
∵AD⊥BC,
∴∠ADF+∠ADG=∠CDF+∠ADF,
∴∠ADG=∠CDF,
∵△ABC与△EFG是等边三角形,
∴△ABC∽△EFG,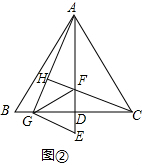 ∴$\frac{AD}{GD}=\frac{CD}{DF}$,
∴$\frac{AD}{GD}=\frac{CD}{DF}$,
∴△ADG∽△CDF;
应用:如图②,
∵△ADG∽△CDF,
∴∠GAD=∠FCD,
∵∠FDC=90°,∠AFH=∠CFD,
∴∠GAD+∠AFH=∠FCD+∠CFD=90°,
∴∠AHF=90°.
点评 本题考查了等边三角形的性质,相似三角形的判定和性质,证明△ADG∽△CDF是解题的关键.

练习册系列答案
相关题目
6.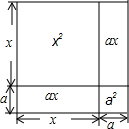 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )| A. | (x+a)(x+a) | B. | x2+a2+2ax | C. | 4(x+a) | D. | (x+a)a+(x+a)x |
13.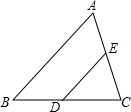 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
10.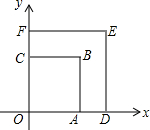 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
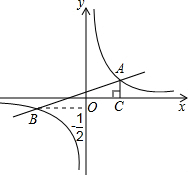 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求:
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求:
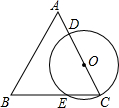 如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).
如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).