题目内容
3.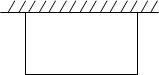 (1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?
(1)如图,要搭建一个矩形的自行车棚,一边靠墙,另外三边围栏材料的总长为60m,怎样围才能使车棚的面积最大?(2)在(1)中,如果可利用的墙壁长为25m,怎样围才能使车棚的面积最大?
题(2)与题(1)的解答完全相同吗?试比较并作出正确的解答,和同学交流.
分析 (1)设长方形的面积为S,利用面积计算方法列出二次函数,用配方法求最大值解答问题;
(2)设长方形的面积为S,利用面积计算方法列出二次函数,用配方法求最大值解答问题.
解答 解:(1)设长方形的面积为Sm2,自行车棚的宽为xm,
由题意得:S=x(60-2x)=-2x2+60x,
即S=-2(x-15)2+450,
∴当x=15时,车棚的面积最大,
答:让与墙垂直的边等于15m,与墙平行的边等于30m车棚的面积最大;
(2)设长方形的面积为Sm2,自行车棚的长(与墙平行的边)为ym,
由题意得:S=y($\frac{60-y}{2}$)=-$\frac{1}{2}$y2+30y,
即:S=-$\frac{1}{2}$(y-30)2+450,
∵a=-$\frac{1}{2}$<0,∴当y≤30时,S随y的增大而增大,
∴当y=25时,车棚的面积最大,
答:让与墙垂直的边等于17.5m,与墙平行的边等于30m时车棚的面积最大;
题(2)与题(1)的解答不完全相同,题(2)要考虑墙的课利用长度,题(1)不用考虑.
点评 本题考查了二次函数在实际生活中的应用,及二次函数求最大值问题,利用配方法求最大值是常用的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.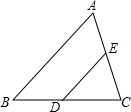 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
 如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )
如图,在△ABC中,点D、E分别是边BC、AC上的点,连结DE,若△EDC∽△ABC,且AE=4,CE=5,则$\frac{CD}{CB}$的值是( )| A. | $\frac{5}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
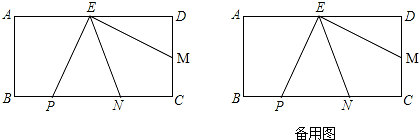
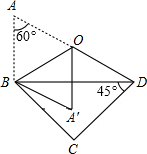 如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么?
如图,一副三角板拼在一起,O为AD的中点,将△ABO沿OB折叠,点A落在A′的位置,点C在直线OA′上吗?为什么? ”可爱吧!表面能展开平面图形“
”可爱吧!表面能展开平面图形“ ”的是圆锥..
”的是圆锥..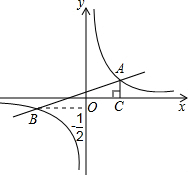 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求:
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$ (m≠0)的图象相交于A、B两点,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴于点C,且AC=1,OC=2.求: