题目内容
如图,在平面直角坐标系中有两点A、B,请回答下列问题:
(1)在图(1)中找出点A、点B关于y轴的对称点D、C,将A、B、C、D四点顺次连接起来,并回答四边形ABCD是什么四边形?(直接回答)
(2)若点P从B点出发,以每秒钟2的速度沿B→C的方向运动,求经过几秒钟后,AP所在的直线将四边形ABCD的面积分成2:3.
(3)在线段BC上有一点E,△ABE是等腰三角形,将直线AE绕点E顺时针旋转45°后与直线DC交于点F,求F点的坐标.(图(2)、(3)、(4)为备用图)

(1)在图(1)中找出点A、点B关于y轴的对称点D、C,将A、B、C、D四点顺次连接起来,并回答四边形ABCD是什么四边形?(直接回答)
(2)若点P从B点出发,以每秒钟2的速度沿B→C的方向运动,求经过几秒钟后,AP所在的直线将四边形ABCD的面积分成2:3.
(3)在线段BC上有一点E,△ABE是等腰三角形,将直线AE绕点E顺时针旋转45°后与直线DC交于点F,求F点的坐标.(图(2)、(3)、(4)为备用图)

考点:一次函数综合题
专题:压轴题
分析:(1)根据题意容易得出四边形ABCD是等腰梯形;
(2)设经过t秒,先求出等腰梯形ABCD的面积,即可求出t的值;
(3)分三种情况讨论:①当AE=BE时,②当AE=AB时,③当BE=BA时,分别求出F的坐标即可.
(2)设经过t秒,先求出等腰梯形ABCD的面积,即可求出t的值;
(3)分三种情况讨论:①当AE=BE时,②当AE=AB时,③当BE=BA时,分别求出F的坐标即可.
解答:
解:(1)如图1所示:四边形ABCD是等腰梯形;

(2)如图2所示:

设经过t秒后,AP所在的直线将四边形ABCD的面积分成2:3;
∵AD=2,BC=8,
∴S等腰梯形ABCD=
(2+8)×3=15,
∴S△ABP=
×2t×3=3t=15×
=6,
∴t=2,
即经过2秒后,AP所在的直线将四边形ABCD的面积分成2:3;
(3)分三种情况讨论:①如图3所示,
根据题意:当AE=BE时,作FG⊥BC于G;

∴点E在AB的垂直平分线上,点E的坐标为(-1,0),
∴∠AEC=90°,
∵∠AEF=45°,
∴∠FEC=45°,
由图形得:∠C=45°,
∴∠EFC=90°,
∵CE=1+4=5,
∴FG=EG=
CE=
,
∴OG=
,∴F(
,
);
②如图4所示,

当AE=AB时,
∵AB=CD,
∴AE=CD,
∵∠ABC=45°,
∴∠AEB=45°,
∴AE∥CD,
∴四边形AECD是平行四边形,
∴CE=AD=2,
∴OE=2,
∴EF=2,
∴F(2,2);
③如图5所示:

当BE=BA时,作FG⊥BC于G,
∵BE=BA=3
,∠ABC=45°,
∴E(3
-4,0),∠AEB=∠EAB=67.5°,
∴OE=3
-4,
∴CE=5-(3
-4)=9-3
,∠CEF=180°-67.5°-45°=67.5°,
∴CE=CF,
∵∠C=45°,
∴△CEF∽△BAE,
∴
=
=
,
∴FG=
,
∴CG=FG=
,
∴OG=4-
=7-
,
∴F(7-
,
-3);
综上所述:点F的坐标为(
,
),或(2,2),或(7-
,
-3).

(2)如图2所示:

设经过t秒后,AP所在的直线将四边形ABCD的面积分成2:3;
∵AD=2,BC=8,
∴S等腰梯形ABCD=
| 1 |
| 2 |
∴S△ABP=
| 1 |
| 2 |
| 2 |
| 5 |
∴t=2,
即经过2秒后,AP所在的直线将四边形ABCD的面积分成2:3;
(3)分三种情况讨论:①如图3所示,
根据题意:当AE=BE时,作FG⊥BC于G;

∴点E在AB的垂直平分线上,点E的坐标为(-1,0),
∴∠AEC=90°,
∵∠AEF=45°,
∴∠FEC=45°,
由图形得:∠C=45°,
∴∠EFC=90°,
∵CE=1+4=5,
∴FG=EG=
| 1 |
| 2 |
| 5 |
| 2 |
∴OG=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
②如图4所示,

当AE=AB时,
∵AB=CD,
∴AE=CD,
∵∠ABC=45°,
∴∠AEB=45°,
∴AE∥CD,
∴四边形AECD是平行四边形,
∴CE=AD=2,
∴OE=2,
∴EF=2,
∴F(2,2);
③如图5所示:

当BE=BA时,作FG⊥BC于G,
∵BE=BA=3
| 2 |
∴E(3
| 2 |
∴OE=3
| 2 |
∴CE=5-(3
| 2 |
| 2 |
∴CE=CF,
∵∠C=45°,
∴△CEF∽△BAE,
∴
| FG |
| 3 |
| CE |
| AB |
9-3
| ||
3
|
∴FG=
9
| ||
| 2 |
∴CG=FG=
9
| ||
| 2 |
∴OG=4-
9
| ||
| 2 |
9
| ||
| 2 |
∴F(7-
9
| ||
| 2 |
9
| ||
| 2 |
综上所述:点F的坐标为(
| 3 |
| 2 |
| 5 |
| 2 |
9
| ||
| 2 |
9
| ||
| 2 |
点评:本题考查了点的坐标、等腰梯形的性质、等腰三角形的性质以及相似三角形的判定与性质;培养学生综合运用定理进行推理和计算解决问题的能力;特别注意(3)中利用分类讨论的方法求解,避免漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 实数a、b在数轴上的位置如图所示,则下列各式正确的是( )
实数a、b在数轴上的位置如图所示,则下列各式正确的是( )| A、a+b>0 |
| B、|a-b|=b-a |
| C、|a|=a |
| D、|b|=b |
已知线段a=1cm,c=4cm,x是a、c的比例中项,则x等于( )
| A、4cm | B、2cm |
| C、-2cm | D、±2cm |
以下列各组数为三角形的边长,能构成直角三角形的是( )
| A、1,2,3 |
| B、5,6,9 |
| C、5,12,13 |
| D、8,10,13 |

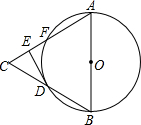 如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于
如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于 如图,A,B两点坐标分别是(3,-1),(3,1),请你画出平面直角坐标系并标出点P(-2,3)的位置.
如图,A,B两点坐标分别是(3,-1),(3,1),请你画出平面直角坐标系并标出点P(-2,3)的位置. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
如图,△ABC≌△DEF,请根据图中提供的信息,写出x=