题目内容
两个相似的五边形,一个各边长分别为1,2,3,4,5,另一个五边形的最长边为8,则后一个五边形的周长为 .
考点:相似多边形的性质
专题:
分析:根据两个相似五边形的最长边的值,可得出它们的相似比,进而可根据相似五边形的周长比等于相似比来求得另一个五边形的周长.
解答:
解:设所求五边形的周长为x,
∵一个五边形的各边长分别为1,2,3,4,5,另一个五边形的最长边为8,
∴两个五边形的相似比=
.
∵第一个五边形的周长=1+2+3+4+5=15,
∴
=
,解得x=24.
故答案为24.
∵一个五边形的各边长分别为1,2,3,4,5,另一个五边形的最长边为8,
∴两个五边形的相似比=
| 5 |
| 8 |
∵第一个五边形的周长=1+2+3+4+5=15,
∴
| 15 |
| x |
| 5 |
| 8 |
故答案为24.
点评:本题考查的是相似多边形的性质,熟知相似多边形周长的比等于相似比是解答此题的关键.

练习册系列答案
相关题目
一元二次方程2x2+5x+3=0的实数根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
 如图,已知△ABC,以AB为直径的⊙O交AC于点D,交BC于点E,若∠C=70°,则∠DOE的度数为
如图,已知△ABC,以AB为直径的⊙O交AC于点D,交BC于点E,若∠C=70°,则∠DOE的度数为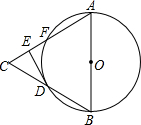 如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于
如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于 如图,A,B两点坐标分别是(3,-1),(3,1),请你画出平面直角坐标系并标出点P(-2,3)的位置.
如图,A,B两点坐标分别是(3,-1),(3,1),请你画出平面直角坐标系并标出点P(-2,3)的位置. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
如图,△ABC≌△DEF,请根据图中提供的信息,写出x= 如图,在Rt△ABC中,∠BCA=90°,CD是斜边AB上的高,若∠A=30°,BD=1cm,则AD=
如图,在Rt△ABC中,∠BCA=90°,CD是斜边AB上的高,若∠A=30°,BD=1cm,则AD=