题目内容
已知抛物线y=2(x+2)2交y轴于点A,交直线y=2x+4于点B、C两点,求S△ABC的值.
考点:二次函数的性质
专题:
分析:根据抛物线的解析式求得A的坐标,联立方程,解方程组即可求得B、C的坐标,然后求得直线BC的解析式求得直线与y轴的交点D的坐标,最后根据S△ABC=S△ABD-S△ACD即可求得S△ABC的值.
解答:
解:∵y=2(x+2)2=2x2+8x+8,
∴A的坐标为(0,8),
解
得
,
,
∴B(-2,0),C(-1,2),
设直线BC的解析式为y=kx+b,交y轴于D,
∴
,解得
,
∴D(0,4),
∴AD=8-4=4,
∴S△ABC=S△ABD-S△ACD=
×4×2-
×4×1=2.
∴A的坐标为(0,8),
解
|
|
|
∴B(-2,0),C(-1,2),
设直线BC的解析式为y=kx+b,交y轴于D,
∴
|
|
∴D(0,4),
∴AD=8-4=4,
∴S△ABC=S△ABD-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了二次函数的性质,函数图象交点、图形面积的求法等知识点.
(1)函数图象交点坐标为两函数解析式组成的方程组的解.
(2)不规则图形的面积通常转化为规则图形的面积的和差.
(1)函数图象交点坐标为两函数解析式组成的方程组的解.
(2)不规则图形的面积通常转化为规则图形的面积的和差.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目

 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. 如图,已知△ABC,以AB为直径的⊙O交AC于点D,交BC于点E,若∠C=70°,则∠DOE的度数为
如图,已知△ABC,以AB为直径的⊙O交AC于点D,交BC于点E,若∠C=70°,则∠DOE的度数为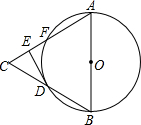 如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于
如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于