题目内容
12. 如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )
如图,在△ABC中,AC=BC,BD⊥AC于点D,以点C为旋转中心,将△BCD顺时针旋转,得到△ACD′.若∠ABD=35°,则∠BCD′的大小为( )| A. | 140° | B. | 145° | C. | 150° | D. | 155° |
分析 直角△ABD中利用三角形内角和定理求得∠BAC的度数,然后根据等边对等角求得∠ABC的度数,则在△ABC中利用三角形内角和定理求得∠BCA的度数,则∠BCD′即可求得.
解答 解:∵BD⊥AC,
∴直角△ABD中,∠BAC=90°-∠ABD=90°-35°=55°,
又∵AC=BC,
∴∠ABC=∠BAC=55°,
∴∠BCA=180°-55°-55°=70°,
又∵∠BCA=∠ACD',
∴∠BCD'=70°+70°=140°.
故选A.
点评 本题考查了旋转的性质以及等腰三角形的性质:等边对等角,正确求得∠BCA的度数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
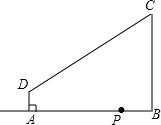 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
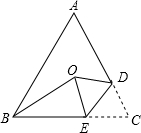 如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.
如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.