题目内容
14.若M是线段AB的黄金分割点(MA>MB),设AB=2cm,则线段MA的长为( )cm.| A. | $\frac{\sqrt{5}-1}{2}$ | B. | 3-$\sqrt{5}$ | C. | 1 | D. | $\sqrt{5}$-1 |
分析 根据黄金分割点的定义,知MA是较长线段;则MA=$\frac{\sqrt{5}-1}{2}$AB,代入数据即可得出MA的长.
解答 解:由于点M为线段AB=2cm的黄金分割点,且MA是较长线段,
则MA=$\frac{\sqrt{5}-1}{2}$AB=($\sqrt{5}$-1)cm.
故选D.
点评 本题考查黄金分割的定义:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.识记黄金分割的公式:较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$,较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$是解题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
2.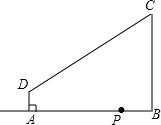 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=2cm,BC=6cm,AB=7cm,点P是从点B出发在射线BA上的一个动点,运动的速度是1cm/s,连结PC、PD.若△PAD与△PBC是相似三角形,则满足条件的点P个数是( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
9.在不透明的盒子中装有3个红球,2个白球,它们除颜色外均相同,则从盒中子任意摸出一个球是白球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..
如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..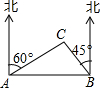 世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.
世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.