题目内容
如图所示，已知△ABC为直角三角形，∠B=90°，若沿图中虚线剪去∠B，则∠1+∠2等于多少度？考点：多边形内角与外角
专题：
分析：首先利用三角形内角和定理计算出∠A+∠C=90°，再根据四边形内角和为360°可得∠1+∠2的度数．
解答：解：∵∠B=90°，
∴∠A+∠C=90°，
∵∠1+∠2+∠A+∠C=360°，
∴∠1+∠2=360°-90°=270°．
∴∠A+∠C=90°，
∵∠1+∠2+∠A+∠C=360°，
∴∠1+∠2=360°-90°=270°．
点评：此题主要考查了多边形的内角和，关键是掌握多边形内角和为360°．
练习册系列答案
相关题目
在数轴上表示下列各数，并用“＜”连接起来．-3.5，-（-2），（-2）2，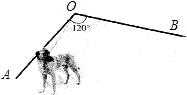
如图，墙OA、OB的夹角∠AOB=120°，一根3m长的绳子一端拴在墙角O处，另一端拴着一只小狗，求小狗可活动的区域的面积．（结果保留π）
下列式子从左到右是因式分解的是（ ）
| A、（x+y）（x-y）=x2-y2 |
| B、x2-2x+3=x（x-2）+3 |
| C、a（x+y）=ax+ay |
| D、a2+2ab+b2=（a+b）2 |