题目内容
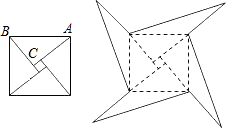 如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是
如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风”所围成的总面积是考点:勾股定理的证明
专题:
分析:先根据勾股定理得到AB的长,根据正方形的面积公式和三角形的面积公式可得中间小正方形的面积,再根据等高的三角形面积比等于底边的比,列式计算即可求解.
解答:解:在直角三角形ACB中,
AB=
=2
,
中间小正方形的面积:
2
×2
-6×4÷2×4
=52-48
=4,
4+6×4÷2×4×2
=4+96
=100.
故答案为:100.
AB=
| 62+42 |
| 13 |
中间小正方形的面积:
2
| 13 |
| 13 |
=52-48
=4,
4+6×4÷2×4×2
=4+96
=100.
故答案为:100.
点评:本题是勾股定理在实际情况中应用,并注意隐含的已知条件来解答此类题.

练习册系列答案
相关题目
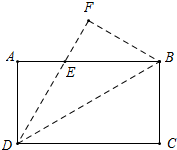 把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.
把一张长方形的纸ABCD沿对角线BD翻折,使得C点落在点F处,DF交AB于E,已知AE=2,DC=6,求∠ADE.
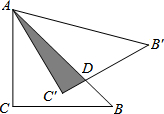 如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6
如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6