题目内容
【题目】在
中，
,以AC为直径的半圆O交于点D，过点D作圆O的切线，交BC于点E，点F是半圆上异于点D的任一动点．
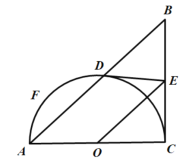
（1）求证：
；
（2）填空：
①若
，则四边形
的面积为________；
②当
的度数是_______时，以
为顶点的四边形为菱形．
【答案】（1）见解析；（2）①
；②30°或60°．
【解析】
（1）连接OD，证明
，得
，利用外角和定理得
，可得
，证得平行；
（2）①连接CD，证明
，求出AC，用勾股定理求出CD，结合
，E为中点，四边形
在BD上的高为CD的一半，可求出面积；
②分为点F在
和
上，根据菱形的性质结合圆的特点，分类讨论即可．
（1）连接DO，则
因为DE是圆的切线,所以
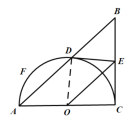
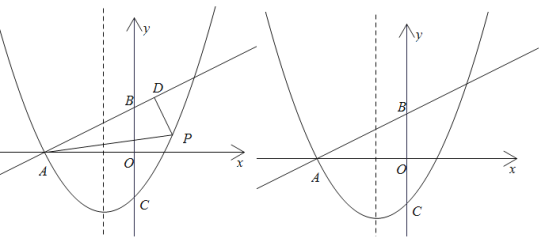
(2) ①连接CD，如图所示：
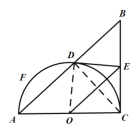
∵AC为直径
∴
°
∵
且
∴
∴
∵
∴
∴
∴
∵
且E为中点
∴
故答案为：
②若点F在上时，如图所示：
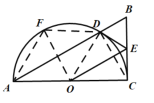
∵AODF为菱形
∴AF=AO
∵AO=OF
∴
为等边三角形
∴
∴
∴
若点F在上，作图如下：
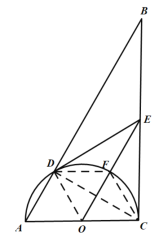
∵AODF为菱形
∴AD=AO
∵AO=OD
∴
为等边三角形
∴
∴
故答案为：30°或60°
名师指导期末冲刺卷系列答案【题目】某商店计划一次性购进甲、乙两种商品共
件，甲、乙两种商品的进价和售价如下表所示：
甲 | 乙 | |
进价（元/件） | 100 | 80 |
售价（元/件） | 150 | 120 |
设购进甲种商品的数量为
件．
（1）设进货成本为
元，求与之间的函数解析式；若购进甲种商品的数量不少于
件，则最低进货成本是多少元？
（2）若除了进货成本，还要支付运费和销售员工工资共
元，为尽快回笼资金，该商店决定对甲种商品进行降价销售，每件甲种商品降价
元
，乙种商品售价不变，设销售完甲、乙两种商品获得的总利润为
元．
①每件甲种商品的利润是 元（用含的代数式表示）
②求关于的函数解析式
③当
时，请你根据的取值范围，说明该商店购进甲种商品多少件时，获得的总利润最大．
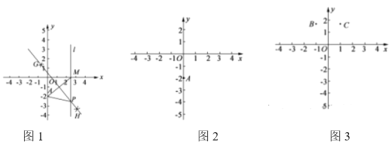
【题目】如图1，在平面直角坐标系中，点A的坐标是
，在x轴上任取一点M．连接AM，分别以点A和点M为圆心，大于
的长为半径作弧，两弧相交于G，H两点，作直线GH，过点M作x轴的垂线l交直线GH于点P．根据以上操作，完成下列问题．
探究：
（1）线段PA与PM的数量关系为________，其理由为：________________．
（2）在x轴上多次改变点M的位置，按上述作图方法得到相应点P的坐标，并完成下列表格：
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
| … |
猜想：
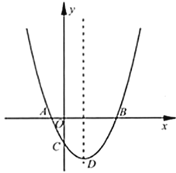
（3）请根据上述表格中P点的坐标，把这些点用平滑的曲线在图2中连接起来；观察画出的曲线L，猜想曲线L的形状是________．
验证：
（4）设点P的坐标是
，根据图1中线段PA与PM的关系，求出y关于x的函数解析式．
应用：
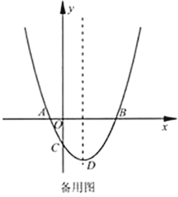
（5）如图3，点
，
，求点D的纵坐标
的取值范围．
