Question

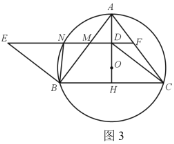
【题目】如图，已知矩形，对角线的垂直平分线分别交，和于点，，．，的延长线交于点，且，连接．

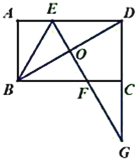
（1）求证：

（2）求证：平分．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）垂直平分线的定义可得∠EOD=90°，根据矩形的性质可得∠FCG=90°，AD//BC，根据平行线的性质可得∠DEO=∠CFG，利用AAS即可证明△DOE≌△GCF；

（2）根据全等三角形的性质可得OE=CF，利用AAS可证明，可得DE=BF，根据线段的和差关系可得AE=CF，即可得出AE=OE，根据到角两边距离相等的点在角的角平分线上即可得出BE平分∠ABD．

（1）∵是垂直平分线，

∴，

∵四边形是矩形，

∴，，

∴，，

∴，

在△DOE和△GCF中，，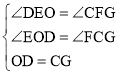

∴△DOE≌△GCF．

（2）由（1）可得：

，

∵是垂直平分线，

∴，

在△EOD和△FOB中，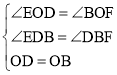

∴，

∴，

∵，

∴AD-DE=BC-BF，即AE=CF，

∴AE=OE，

∵∠A=∠BOE=90°，

∴平分．