题目内容
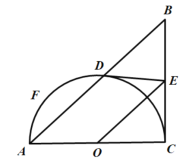
【题目】如图,⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 为直径,点
为直径,点![]() 是⊙
是⊙![]() 外一点,且
外一点,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
⑴.证明:![]() =
=![]() ;
;
⑵.若![]() ,证明:
,证明:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑶.在⑵的条件下,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ;若
;若![]() ,求
,求![]() 的长.
的长.
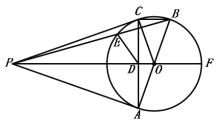
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]()
【解析】
(1)连接CO,易证△PCO≌△PAO,得PO为∠APC的角平分线,根据条件证出F为优弧![]() 中点,即可证明
中点,即可证明![]() =
=![]() ;
;
(2)因为AB是直径,所以∠ACB=90°,由tan∠ABC=![]() 可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC=
可求得∠ABC的正弦和余弦,设⊙O的半径为r,则AB=2r,根据三角函数表示出BC,AC的长度,由勾股定理表示出OD的长度,易得PA=PC=![]() ,
,![]() ,PO=PD+OD=3r,由
,PO=PD+OD=3r,由![]() 可得PA⊥OA,即可证明
可得PA⊥OA,即可证明![]() 是⊙
是⊙![]() 的切线;
的切线;
(3)连接AE,过E作EN⊥PD于N,过B作BH⊥PF于H,由(2)可得,![]() ,PB=
,PB=![]() ,证出△PEA∽△PAB,可得
,证出△PEA∽△PAB,可得![]() ,证出四边形BCDH是矩形,得BH=CD=
,证出四边形BCDH是矩形,得BH=CD=![]() ,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得
,在Rt△BPH和Rt△PEN中表示出sin∠BPH,可得![]() ,
,![]() ,ND=PD-PN=
,ND=PD-PN=![]() ,在Rt△NED中,DE=
,在Rt△NED中,DE=![]() ,代入r=3即可
,代入r=3即可
解:(1)证明:如图,连接CO,
在△PCO和△PAO中,
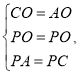
∴△PCO≌△PAO(SSS),
∴∠CPO=∠APO,即PO为∠APC的角平分线,
∵PA=PC,
∴CD=AD,PF⊥AC,
∵AC为⊙O的弦,PF过圆心O,
∴F为优弧![]() 中点,
中点,
∴![]() =
=![]() ,
,
(2)证明:∵AB是⊙O的直径,且弦AB所对圆周角为∠ACB,
∴∠ACB=90°,
∵tan∠ABC=![]() ,
,
∴sin∠ABC=![]() ,cos∠ABC=
,cos∠ABC=![]() ,
,
设⊙O的半径为r,则AB=2r,
∴BC=ABcos∠ABC=![]() ,AC=ABsin∠ABC=
,AC=ABsin∠ABC=![]() ,
,
∴![]() ,
,
∵PA=PC=![]() AB,
AB,
∴PA=PC=![]() ,
,
∴![]() ,
,
∴PO=PD+OD=3r,
∴![]() ,即PA⊥OA,
,即PA⊥OA,
又∵OA是⊙O半径,
∴PA是⊙O的切线;
(3)由(2)可得![]() ,
,
∴![]() ,
,
在Rt△PBA中,![]() ,连接AE,可得∠AEB=90°,
,连接AE,可得∠AEB=90°,
∴∠PEA=∠PAB=90°,又∠APE=∠APB,
∴△PEA∽△PAB,
∴![]() ,
,
∴![]() ,
,
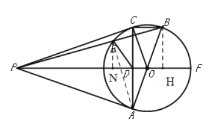
过E作EN⊥PD于N,过B作BH⊥PF于H,如图所示,
∴∠BCD=∠CDF=∠BHD=90°,
∴四边形BCDH是矩形,
∴BH=CD=![]() ,
,
在Rt△BPH中,sin∠BPH=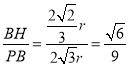 ,
,
在Rt△PEN中,sin∠BPH=![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴ND=PD-PN=![]() ,
,
在Rt△NED中,DE=![]() ,
,
∵![]() ,
,
∴DE=![]() .
.

 阅读快车系列答案
阅读快车系列答案