若x2-mx+$\frac{49}{25}$=(x+n)2.则m+n的值为±$\frac{7}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

19．若x²-mx+$\frac{49}{25}$=（x+n）²，则m+n的值为±$\frac{7}{5}$．

分析将（x²-mx+$\frac{49}{25}$）利用完全平方公式进行配方，然后对应常数相等即可得到m、n的值，所以代入求值即可．

解答解：x²-mx+$\frac{49}{25}$=（x±$\frac{7}{5}$）²，
则m=-$\frac{14}{5}$，n=$\frac{7}{5}$或m=$\frac{14}{5}$，n=-$\frac{7}{5}$．
所以m+n=-$\frac{14}{5}$+$\frac{7}{5}$=-$\frac{7}{5}$或m+n=$\frac{14}{5}$-$\frac{7}{5}$=$\frac{7}{5}$．
综上所述m+n=±$\frac{7}{5}$．
故答案是：±$\frac{7}{5}$．

点评本题考查了配方法的应用．二次三项式是完全平方式，则常数项是一次项系数一半的平方．

练习册系列答案

时习之期末加寒假系列答案

寒假作业假期园地中原农民出版社系列答案

10．下列说法正确的有（　　）个
（1）任意两个矩形都相似（2）任意两个正方形都相似
（3）任意两个等边三角形都相似（4）任意两个菱形都相似．

7．直角△ABC中，∠C=90°，点D、E分别是△ABC上的点，点P是一个动点，令∠PEB=∠2，∠DPE=∠α．
（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2的度数；
（2）如图（2）所示，若点P在边AB上运动，请直接写出∠α、∠1、∠2之间的数量关系关系：∠1+∠2=90+∠α；
（3）如图（3）所示，若点P运动到边AB的延长线上，请直接写出∠α、∠1、∠2之间的数量关系关系：∠1=90°+∠2+∠α；
（4）如图（4）所示，若点P运动到△ABC形外，请直接写出∠α、∠1、∠2之间的数量关系：∠2=90°+∠1-∠α．

14．解不等式，并在数轴上表示解集．
（1）3x-1＜2x+1；
（2）$\frac{2x-1}{3}≤\frac{3x-4}{6}$．

4．

如图，四边形ABCD是一个矩形，⊙C的半径是2，CF=4，EF=2，CE⊥EF于E，则图中阴影部分的面积为$\frac{4π}{3}$．

11．

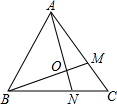在等边△ABC中，M是AC上一点，N是BC上的一点，且AM=BN，∠MBC=25°，AN与BM交于点O，则∠MON的度数为（　　）

	A．	$\sqrt{（-9）（-4）}=\sqrt{-9}•\sqrt{-4}=（-3）（-2）=6$		B．	$\sqrt{8}-\sqrt{2}=\sqrt{2}$
	C．	$\sqrt{{3^2}+{4^2}}=3+4=7$		D．	$\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$

9．下列各式中与x³ⁿ⁺¹相等的是（　　）

（x³）ⁿ⁺¹

（xⁿ⁺¹）³

x³•xⁿ•x

x•x³ⁿ

试题分类