题目内容
14．
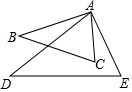如图，在△ABC和△ADE中，$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，∠BAD=20°，求∠CAE的度数．
分析 由在△ABC和△ADE中，$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，可证得△ABC∽△ADE，然后由相似三角形的对应角相等，求得答案．
解答 解：∵在△ABC和△ADE中，$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠CAE=∠BAD=20°．
点评 此题考查了相似三角形的判定与性质．注意证得△ABC∽△ADE是关键．
练习册系列答案
相关题目
5．绝对值不小于1，而小于4的所有的整数有（ ）
| A． | ±1，±2，±3，±4 | B． | ±2，±3 | C． | ±1，±2，±3 | D． | ±2，±3，±4 |
9．下列多项式相乘，不能用平方差公式计算的是（ ）
| A． | （x-2y）（2y+x） | B． | （2y-x）（-x-2y） | C． | （x-2y）（-x-2y） | D． | （-2y-x）（x+2y） |
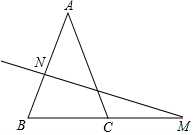已知：如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．