题目内容
14．
如图是一张月历表，在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数（如2，3，9，10）．如果圈出的4个数中最大数与最小数的积为128，则这4个数中最小的数是8．
分析 根据题意分别表示出最小数与最大数，进而利用最大数与最小数的积为128得出等式求出答案．
解答 解：设这4个数中最小数是x，则最大数为：x+8，根据题意可得：
x（x+8）=128，
整理得：x2+8x-128=0，
（x-8）（x+16）=0，
解得：x1=8，x2=-16，
则这4个数中最小的数是8．
故答案为：8．
点评 此题主要考查了一元二次方程的应用，根据题意正确表示出最大数是解题关键．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
5．
如图，四边形ABCD中，AB∥CD，AB=CD，E、F是对角线BD上的两点，如果再添加一个条件，使△ABE≌△CDF，则添加的条件不能是（ ）
如图，四边形ABCD中，AB∥CD，AB=CD，E、F是对角线BD上的两点，如果再添加一个条件，使△ABE≌△CDF，则添加的条件不能是（ ）| A． | AE=CF | B． | BE=FD | C． | BF=DE | D． | ∠1=∠2 |
2．
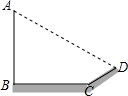如图，某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上，量的CD=8米，BC=20米，斜坡CD的坡度比为1：$\sqrt{3}$，且此时测得1米杆的影长为2米，则电线杆的高度为（ ）
如图，某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上，量的CD=8米，BC=20米，斜坡CD的坡度比为1：$\sqrt{3}$，且此时测得1米杆的影长为2米，则电线杆的高度为（ ）| A． | （14+2$\sqrt{3}$）米 | B． | 28米 | C． | （7+$\sqrt{3}$）米 | D． | 9米 |
如图，a，b为数轴上的两点表示的有理数，在a+b，a-b，b-a，ab，|a-b|，|b|-|a|中负数的个数有（ ）
19．将下列长度的三根木棒首尾顺次连接，能组成三角形的是（ ）
| A． | 1，2，3 | B． | 3，4，5 | C． | 2，5，8 | D． | 3，6，9 |
6．
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①abc＞0；②4a-2b+c＞0；③2a-b＞0；④a＞-1；⑤b2+8a＞4ac．其中正确的有（ ）
如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①abc＞0；②4a-2b+c＞0；③2a-b＞0；④a＞-1；⑤b2+8a＞4ac．其中正确的有（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
3．
如图，在平面直角坐标系中，已知A（0，$\sqrt{3}$），B（-2，-$\sqrt{3}$），△ABC是等边三角形，AD是BC边上的高，则点C的坐标是（ ）
如图，在平面直角坐标系中，已知A（0，$\sqrt{3}$），B（-2，-$\sqrt{3}$），△ABC是等边三角形，AD是BC边上的高，则点C的坐标是（ ）| A． | （2，-$\sqrt{3}$） | B． | （-2，$\sqrt{3}$） | C． | （2，-2） | D． | （-2，2） |