题目内容
2.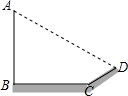 如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )
如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )| A. | (14+2$\sqrt{3}$)米 | B. | 28米 | C. | (7+$\sqrt{3}$)米 | D. | 9米 |
分析 根据已知条件,过D分别作BC、AB的垂线,设垂足为E、F;在Rt△DCE中,已知斜边CD的长和斜坡CD的坡度比为1:$\sqrt{3}$,得出∠DCE的度数,满足解直角三角形的条件,可求出DE、CE的长.即可求得DF、BF的长;在Rt△ADF中,已知了“1米杆的影长为2米”,即坡面AD的坡度为$\frac{1}{2}$,根据DF的长,即可求得AF的长,AB=AF+BF.
解答  解:如图所示:过D作DE垂直BC的延长线于E,且过D作DF⊥AB于F,
解:如图所示:过D作DE垂直BC的延长线于E,且过D作DF⊥AB于F,
∵在Rt△DEC中,CD=8,斜坡CD的坡度比为1:$\sqrt{3}$,
∴∠DCE=30°,
∴DE=4米,CE=4$\sqrt{3}$米,
∴BF=4米,DF=20+4$\sqrt{3}$(米),
∵1米杆的影长为2米,
∴$\frac{AF}{20+4\sqrt{3}}$=$\frac{1}{2}$,
则AF=(10+2$\sqrt{3}$)米,
AB=AF+BF=10+2$\sqrt{3}$+4=(14+2$\sqrt{3}$)米,
∴电线杆的高度(14+2$\sqrt{3}$)米.
故选:A.
点评 本题考查了解直角三角形的应用,关键是设法化归为解直角三角形问题,添加辅助线,构造出直角三角形求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.化简a2•a3的结果是( )
| A. | a-1 | B. | a | C. | a5 | D. | a6 |
10. 如图,点A,B,C在同一条直线上,则图中的线段共有( )
如图,点A,B,C在同一条直线上,则图中的线段共有( )
 如图,点A,B,C在同一条直线上,则图中的线段共有( )
如图,点A,B,C在同一条直线上,则图中的线段共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
17. 如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )
如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )
 如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )
如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
7.以下等式变形不正确的是( )
| A. | 由x+2=y+2,得到x=y | B. | 由2a-3=b-3,得到2a=b | ||
| C. | 由am=an,得到m=n | D. | 由m=n,得到2am=2an |
12. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )| A. | 54° | B. | 60° | C. | 66° | D. | 76° |
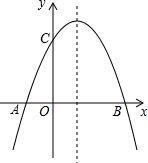 抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点.
抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点. 如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,则这4个数中最小的数是8.
如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,则这4个数中最小的数是8.