题目内容
1.已知二次函数y=a(x+m)2+k的图象经过点(0,-1),且其顶点坐标为(1,2)(1)求这个二次函数的表达式;
(2)判断点(3,-9)是否在这个函数的图象上;
(3)若点A(100,y1),B(101,y2)是该函数图象上的两点,试比较y1与y2大小;
(4)如果要通过适当的平移,使得这个函数的图象与x轴只有一个公共点,那么应该怎样平移?
分析 (1)根据抛物线的顶点坐标设出,抛物线的解析式为:y=a(x-1)2+2,再把(0,-1)代入,求出a的值,即可得出二次函数的解析式.
(2)代入(3,-9)即可判断;
(3)根据函数的性质即可判断;
(4)根据顶点坐标和开口方向即可得出平移的方向和大小.
解答 解:(1)设抛物线的解析式为:y=a(x-1)2+2,
把(0,-1)代入解析式得a+2=-1,解得a=-3
则抛物线的解析式为:y=-3(x-1)2+2.
(2)把x=3代入y=-3(x-1)2+2得y=-10≠-9,
所以,点(3,-9)不在这个函数的图象上;
(3)∵二次函数的图象的对称轴为x=1,a=-3<0,
∴在对称轴的右侧y随x的增大二减小,
∵101>100>1,
∴y1>y2;
(4)∵顶点坐标为(1,2),开口向下,
要使函数的图象与x轴只有一个公共点,则顶点的纵坐标为0,
∴平移后的顶点为(1,0),
∴向下平移2个单位,使得这个函数的图象与x轴只有一个公共点.
点评 本题考查了待定系数法求二次函数的解析式,二次函数图象上点的坐标特征,二次函数的性质以及图象与几何变换.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.下列调查方式中,采用了“普查”方式的是( )
| A. | 调查某品牌手机的市场占有率 | |
| B. | 调查电视网(芈月传)在全国的收视率 | |
| C. | 调查我校初一(1)班的男女同学的比率 | |
| D. | 调查某型号节能灯泡的使用寿命 |
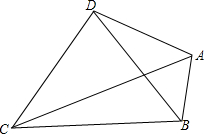 如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6.
如图,四边形ABCD中,AC、BD为对角线,AC=10,BC=6,∠ADB=∠ABD=∠ACB=30°,那么线段CD的长为10$\sqrt{3}$-6. 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BF⊥CD于点F,AB交CD于点E,求证:AD=BF-DF.