Question

12．在直角坐标系中，一条直线经过A（-1，5），P（-2，a），B（3，-3）．
（1）求a的值；
（2）设这条直线与y轴相交于点D，求△AOB的面积．

Answer 1

分析 （1）根据点A、B的坐标利用待定系数法即可求出直线AB的解析式，再利用一次函数图象上点的坐标即可求出a值；
（2）将x=0代入直线AB的解析式中求出点D的坐标，再根据S_△AOB=S_△AOD+S_△BOD利用三角形的面积公式即可得出结论．

解答 解：（1）设直线AB的解析式为y=kx+b，
将点A（-1，5）、B（3，-3）代入y=kx+b中，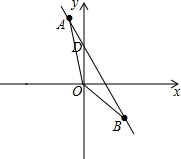
得：$\left\{\begin{array}{l}{5=-k+b}\\{-3=3k+b}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$，
∴直线AB的解析式为y=-2x+3．
当x=-2时，y=-2×（-2）+3=7，
∴a=7．
（2）当x=0时，y=-2×0+3=3，
∴S_△AOB=S_△AOD+S_△BOD=$\frac{1}{2}$OD•（x_B-x_A）=$\frac{1}{2}$×3×[3-（-1）]=6．

点评 本题考查了待定系数法求函数解析式、一次函数图象上点的坐标特征以及三角形的面积，解题的关键是：（1）利用待定相似法求出函数解析式；（2）将△AOB分成△AOD和△BOD．本题属于基础题，难度不大，解决该题型题目时，根据点的坐标利用待定系数法求出函数解析式是关键．