题目内容
阅读下列材料:
解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x-y=2,∴x=y+2
又∵x>1,∴y+2>1.
∴y>-1.
又∵y<0,∴-1<y<0. …①
同理得:1<x<2. …②
由①+②得-1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x-y=3,且x>2,y<1,则x+y的取值范围是 .
(2)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示).
解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解∵x-y=2,∴x=y+2
又∵x>1,∴y+2>1.
∴y>-1.
又∵y<0,∴-1<y<0. …①
同理得:1<x<2. …②
由①+②得-1+1<y+x<0+2
∴x+y的取值范围是0<x+y<2
请按照上述方法,完成下列问题:
(1)已知x-y=3,且x>2,y<1,则x+y的取值范围是
(2)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示).
考点:一元一次不等式组的应用
专题:阅读型
分析:(1)根据阅读材料所给的解题过程,直接套用解答即可;
(2)理解解题过程,按照解题思路求解.
(2)理解解题过程,按照解题思路求解.
解答:解:(1)∵x-y=3,
∴x=y+3,
又∵x>2,
∴y+3>2,
∴y>-1.
又∵y<1,
∴-1<y<1,…①
同理得:2<x<4,…②
由①+②得-1+2<y+x<1+4
∴x+y的取值范围是1<x+y<5;
(2)∵x-y=a,
∴x=y+a,
又∵x<-1,
∴y+a<-1,
∴y<-a-1,
又∵y>1,
∴1<y<-a-1,…①
同理得:a+1<x<-1,…②
由①+②得1+a+1<y+x<-a-1+(-1),
∴x+y的取值范围是a+2<x+y<-a-2.
∴x=y+3,
又∵x>2,
∴y+3>2,
∴y>-1.
又∵y<1,
∴-1<y<1,…①
同理得:2<x<4,…②
由①+②得-1+2<y+x<1+4
∴x+y的取值范围是1<x+y<5;
(2)∵x-y=a,
∴x=y+a,
又∵x<-1,
∴y+a<-1,
∴y<-a-1,
又∵y>1,
∴1<y<-a-1,…①
同理得:a+1<x<-1,…②
由①+②得1+a+1<y+x<-a-1+(-1),
∴x+y的取值范围是a+2<x+y<-a-2.
点评:本题考查了一元一次不等式组的应用,解答本题的关键是仔细阅读材料,理解解题过程,难度一般.

练习册系列答案
相关题目
在12:30时,钟表上的时针与分针所成的角是( )
| A、直角 | B、钝角 | C、平角 | D、锐角 |
 如图,Rt△ABC中,∠C=90°,过C作CD⊥AB于D,求证:CD2=AD•DB.
如图,Rt△ABC中,∠C=90°,过C作CD⊥AB于D,求证:CD2=AD•DB. 在平面直角坐标系中(如图),已知抛物线y=
在平面直角坐标系中(如图),已知抛物线y=
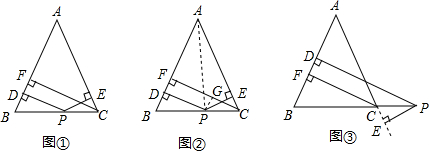
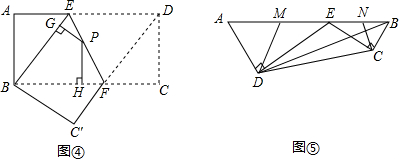
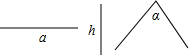 已知三角形的一边a,垂直于a的高h,以及a的对角α,你认为只利用尺规作图能作出这个三角形吗?
已知三角形的一边a,垂直于a的高h,以及a的对角α,你认为只利用尺规作图能作出这个三角形吗?