题目内容
 如图,Rt△ABC中,∠C=90°,过C作CD⊥AB于D,求证:CD2=AD•DB.
如图,Rt△ABC中,∠C=90°,过C作CD⊥AB于D,求证:CD2=AD•DB.考点:相似三角形的判定与性质
专题:证明题
分析:由∠BCA为直角,得到∠BCD与∠ACD互余,再由CD垂直AB,得到∠BDC=∠ADC=90°,且∠A与∠ACD互余,利用同角的余角相等得到一对角相等,进而确定出三角形ACD与三角形CBD相似,由相似得比例,变形即可得证.
解答:证明:∵∠BCA=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴
=
,
则CD2=AD•DB.
∴∠BCD+∠ACD=90°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴
| CD |
| BD |
| AD |
| CD |
则CD2=AD•DB.
点评:此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,水平放置的长方体的底面是边长为3和5的长方形,它的左视图的面积为12,则长方体的体积等于
如图,水平放置的长方体的底面是边长为3和5的长方形,它的左视图的面积为12,则长方体的体积等于 如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G、H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G、H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).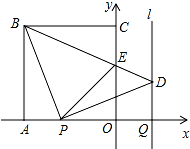 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).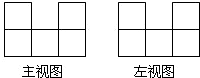 在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为
在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的个数为n,则n的最小值为