题目内容
在“黄袍山国家油茶产业示范园”建设中,某农户计划购买甲、乙两种油茶树苗共1000株.已知乙种树苗比甲种树苗每株贵3元,且用100元钱购买甲种树苗的株数与用160元钱购买乙种树苗的株数刚好相同.
(1)求甲、乙两种油茶树苗每株的价格;
(2)如果购买两种树苗共用5600元,那么甲、乙两种树苗各买了多少株?
(3)调查统计得,甲、乙两种树苗的成活率分别为90%,95%.要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
(1)求甲、乙两种油茶树苗每株的价格;
(2)如果购买两种树苗共用5600元,那么甲、乙两种树苗各买了多少株?
(3)调查统计得,甲、乙两种树苗的成活率分别为90%,95%.要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
考点:一次函数的应用,二元一次方程组的应用,一元一次不等式的应用
专题:应用题
分析:(1)设甲、乙两种油茶树苗每株的价格分别为x元,y元,根据条件中树苗的数量与单价之间的关系建立二元一次方程组求出其解即可;
(2)设购买甲种树苗a株,乙种树苗则购买(1000-a)株,根据两种树苗共用5600元建立方程求出其解即可;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,根据条件建立不等式和W与b的函数关系式,由一次函数的性质就可以得出结论.
(2)设购买甲种树苗a株,乙种树苗则购买(1000-a)株,根据两种树苗共用5600元建立方程求出其解即可;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,根据条件建立不等式和W与b的函数关系式,由一次函数的性质就可以得出结论.
解答:解:(1)设甲、乙两种油茶树苗每株的价格分别为x元,y元,由题意得
,
解得:
.
答:甲、乙两种油茶树苗每株的价格分别为5元,8元;
(2)设甲购买了a株,乙购买了(1000-a)株,由题意得
5a+8(1000-a)=5600,
解得:a=800,
∴乙种树苗购买株数为:1000-800=200株.
答:甲种树苗800株,乙种树苗购买200株;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,由题意得
90%b+95%(1000-b)≥1000×92%,
∴b≤600.
W=5b+8(1000-b)=-3b+8000,
∴k=-3<0,
∴W随b的增大而减小,
∴b=600时,W最低=6200元.
答:购买甲种树苗600株,乙种树苗400株费用最低,最低费用是6200元.
|
解得:
|
答:甲、乙两种油茶树苗每株的价格分别为5元,8元;
(2)设甲购买了a株,乙购买了(1000-a)株,由题意得
5a+8(1000-a)=5600,
解得:a=800,
∴乙种树苗购买株数为:1000-800=200株.
答:甲种树苗800株,乙种树苗购买200株;
(3)设甲种树苗购买b株,则乙种树苗购买(1000-b)株,购买的总费用为W元,由题意得
90%b+95%(1000-b)≥1000×92%,
∴b≤600.
W=5b+8(1000-b)=-3b+8000,
∴k=-3<0,
∴W随b的增大而减小,
∴b=600时,W最低=6200元.
答:购买甲种树苗600株,乙种树苗400株费用最低,最低费用是6200元.
点评:本题考查了列二元一次方程组解实际问题的运用,一元一次不等式解实际问题的运用,一次函数的解析式的运用,解答时由方程组求出两种树苗的单价是关键.

练习册系列答案
相关题目
 如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G、H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).
如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G、H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).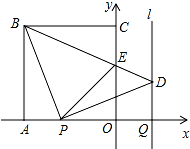 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s). 某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.
某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.