题目内容

如图所示，ABCD是长方形地面，长AB=20m，宽AD=10m．中间竖有一堵砖墙高MN=2m．一只蚂蚱从A点爬到C点，它必须翻过中间那堵墙，则它至少要走
 
m的路程．
考点：平面展开-最短路径问题
专题：探究型
分析：连接AC，利用勾股定理求出AC的长，再把中间的墙平面展开，使原来的矩形长度增加而宽度不变，求出新矩形的对角线长即可．
解答：解：如图所示，将图展开，图形长度增加2MN，
原图长度增加4米，则AB=20+4=24m，
连接AC，
∵四边形ABCD是长方形，AB=24m，宽AD=10m，
∴AC=
AB2+BC2
=
242+102
=
676
=26m，
∴蚂蚱从A点爬到C点，它至少要走26m的路程．
故答案为：26m．
点评：本题考查的是平面展开最短路线问题及勾股定理，根据题意画出图形是解答此题的关键．
练习册系列答案
相关题目
一个三角形的三条边长分别是a，b，c（a，b，c都是质数），且a+b+c=16，则这个三角形的形状是
 
．
定义新运算△为：a△b=ab+2a+2b+2，如果x△2△2△2△2△2=5118，则x=（　　）
A、1B、2C、3D、无法确定
方程x2+4x+k=0有两个实根x1和x2，且（x12+4x1）（x22+4x2）=25，则k的值是（　　）
A、±5B、5
C、-5D、不存在这样的k值
若数组（x，y，z）满足下列三个方程：
xy
x+y+z
=1、
zx
x+y+z
=
3
2
、
yz
x+y+z
=3，则xyz=
 
．
已知
60
(x+1)(x-2)(x+3)
=
A
x+1
 +
B
x-2
+
C
x+3
，其中A，B，C为常数，则A+B+C=
 
．
不超过201的自然数中，至少有两个数字相同的奇数的个数为（　　）
A、25B、24C、23D、22
设n=120120120120，则n2（用10进制表示）的各位数字和是（　　）
A、60B、81C、90D、99
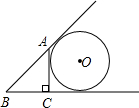如图AC⊥BC于C，BC=a，CA=b，AB=c，⊙O与直线AB、BC、AC都相切，则⊙O的半径为（　　）
A、
a+b-c
2
B、
b+c-a
2
C、
a+b+c
2
D、
a+c-b
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网